
【题目】如图所示,(1)∠BED与∠CBE是直线________,________被直线________所截形成的________角;
(2)∠A与∠CED是直线________,________被直线________所截形成的________角;
(3)∠CBE与∠BEC是直线________,________被直线________所截形成的________角;
(4)∠AEB与∠CBE是直线________,________被直线________所截形成的________角.

【答案】DE BC BE 内错 AD DE AC 同位 BC EC BE 同旁内 AE BC BE 内错
【解析】
根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角分别进行分析即可.
(1)∠BED与∠CBE是直线DE,CB被直线EB所截成的内错角;
(2)∠A与∠CED是直线AD,DE被直线AC所截成的同位角;
(3)∠CBE与∠BEC是直线CB,CE被直线BE所截成的同旁内角;
(4)∠AEB与∠CBE是直线AE,BC被直线EB所截成的内错角。


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G. 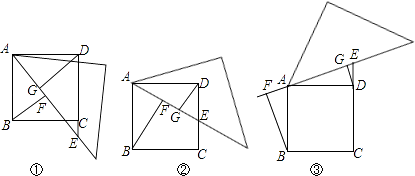
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.内错角相等,两直线平行).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
上述过程中判定依据错误的是( )
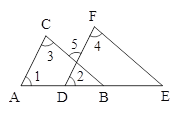
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 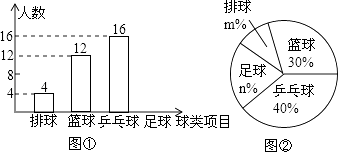
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE. 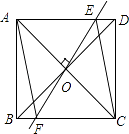
(1)求证:四边形AECF是菱形
(2)若AB=3,BC=4,则菱形AECF的周长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了 ![]() ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
A.![]() =
= ![]() ×
× ![]()
B.![]() =
= ![]() ×
× ![]()
C.![]() +
+ ![]() =
= ![]()
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树形图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com