练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】列方程解应用题：

    为了缓解北京市西部地区的交通拥堵现象，市政府决定修建本市的第一条磁浮地铁线路﹣﹣“S1线”．该线路连接北京城区与门头沟，西起石门营，向东经苹果园，终点至慈寿寺与6号线和10号线相接．为使该工程提前4个月完成，在保证质量的前提下，必须把工作效率提高10%．问原计划完成这项工程需用多少个月．

    【答案】原计划完成这项工程用44个月．

    【解析】

    本题的等量关系是：原计划用的时间=实际用的时间+4个月．实际的工作效率=原计划的工作效率×（1+10%），由此可得出方程来求出未知数．

    解：设原计划完成这项工程用x个月，则实际完成这项工程用（x﹣4）个月．

    根据题意有：

    解得：x=44．

    经检验：x=44是原方程的解．

    答：原计划完成这项工程用44个月．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB+BC=BE，则∠B的度数是（　　）

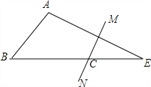
    A. 45° B. 60° C. 50° D. 55°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O中，点A为 中点，BD为直径，过A作AP∥BC交DB的延长线于点P．
    （1）求证：PA是⊙O的切线；
    （2）若 ，AB=6，求sin∠ABD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用22米长的篱笆和6米长的围墙围成一个矩形鸡舍．
    （1）爸爸的方案是：一面是墙，另外三面是篱笆，求爸爸围成的鸡舍面积最大是多少？
    （2）小明的方案是：把有墙的一面用篱笆加长作为一边，另外三面也是篱笆，要使围成的鸡舍面积最大，求有墙的一面应该再加长几米长的篱笆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C为⊙O上的一点，P为直径AB延长线上的一点，BH⊥CP于H交⊙O于D，∠PBH=2∠PAC．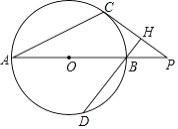
    （1）求证：PC是⊙O的切线；
    （2）若sin∠P= ，求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，圆D与y轴相切于点C（0，4），与x轴相交于A、B两点，且AB=6．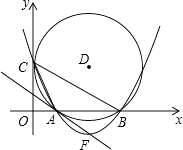

    （1）则D点的坐标是 （ ， ），圆的半径为；
    （2）sin∠ACB=；经过C、A、B三点的抛物线的解析式；
    （3）设抛物线的顶点为F，证明直线FA与圆D相切；
    （4）在x轴下方的抛物线上，是否存在一点N，使△CBN面积最大，最大值是多少，并求出N点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学习小组五名同学在期末模拟考试（满分为120）的成绩如下：100、100、x、x、80．已知这组数据的中位数和平均数相等，那么整数x的值可以是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=4，AD=2，点E、F都对角线AC上，且AE=EF=FC，则线段BE和DF的距离为（ ）
    A.
    B.1
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=x+3分别交x，y轴于点D，C，点B在x轴上，OB=OC，过点B作直线m∥CD．点P、Q分别为直线m和直线CD上的动点，且点P在x轴的上方，满足∠POQ=45°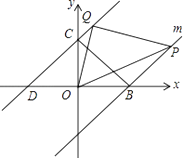

    （1）则∠PBO=度；
    （2）问：PBCQ的值是否为定值？如果是，请求出该定值；如果不是，请说明理由；
    （3）求证：CQ2+PB2=PQ2 ．

    查看答案和解析>>

    同步练习册答案