练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB+BC=BE，则∠B的度数是（　　）

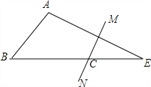
    A. 45° B. 60° C. 50° D. 55°

    【答案】C

    【解析】

    试题利用线段垂直平分线的性质知∠E=∠EAC AC=CE，等量代换得AB=CE=AC，利用三角形的外角性质得∠B=∠ACB=2∠E，从而根据三角形的内角和计算．

    解：连接AC

    ∵CM⊥AE

    ∴∠E=∠EAC AC=CE（线段垂直平分线的性质）

    ∵AB+BC=BE（已知）

    BC+CE=BE

    ∴AB=CE=AC（等量代换）

    ∴∠B=∠ACB=2∠E（外角性质）

    ∵∠B+∠E+105°=180°（三角形内角和）

    ∴∠B+∠B+105°=180°

    解得∠B=50°．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算（小数部份无条件舍去）．
    （1）下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，

    电量（度）

    电费（元）

    A

    240

    B

    合计

    90


    （2）若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中有一正方形AOBC，反比例函数 经过正方形AOBC对角线的交点，半径为（4﹣2 ）的圆内切于△ABC，则k的值为 ．

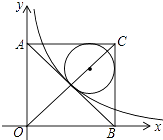
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC沿角平分线BD所在直线翻折，顶点A恰好落在边BC的中点E处，AE=BD，那么tan∠ABD= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲，乙两辆汽车先后从A地出发到B地，甲车出发1小时后，乙车才出发，如图所示的l1和l2表示甲，乙两车相对于出发地的距离y（km）与追赶时间x（h）之间的关系：

    （1）哪条线表示乙车离出发地的距离y与追赶时间x之间的关系？

    （2）甲，乙两车的速度分别是多少？

    （3）试分别确定甲，乙两车相对于出发地的距离y（km）与追赶时间x（h）之间的关系式；

    （4）乙车能在1.5小时内追上甲车吗？若能，说明理由；若不能，求乙车出发几小时才能追上甲？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，DE是边AB的垂直平分线，交AB于E、交AC于D，连接BD．

    （1）若∠ABC＝∠C，∠A＝40°，求∠DBC的度数；

    （2）若AB＝AC，且△BCD的周长为18cm，△ABC的周长为30cm，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】
    （1）当一次性购物标价总额是300元时，甲、乙超市实付款分别是多少？
    （2）当标价总额是多少时，甲、乙超市实付款一样？
    （3）小王两次到乙超市分别购物付款198元和466元，若他只去一次该超市购买同样多的商品，可以节省多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：﹣2﹣1+（ ﹣π）0﹣| ﹣2|﹣2cos30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    为了缓解北京市西部地区的交通拥堵现象，市政府决定修建本市的第一条磁浮地铁线路﹣﹣“S1线”．该线路连接北京城区与门头沟，西起石门营，向东经苹果园，终点至慈寿寺与6号线和10号线相接．为使该工程提前4个月完成，在保证质量的前提下，必须把工作效率提高10%．问原计划完成这项工程需用多少个月．

    查看答案和解析>>

    同步练习册答案