
【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

【答案】(1)l2表示乙车离出发地的距离y与追赶时间x之间的关系;(2)甲车的速度为60km/h,乙车的速度为90km/h;(3)y1=60x+60;y2=90x;(4)乙车不能在1.5小时内追上甲车.乙车追上甲车时,乙车行驶了2小时.
【解析】
(1)通过分析函数图象就可以得出l2表示B车离出发地的距离y与追赶时间x之间的关系;
(2)根据速度=路程÷时间就可以求出两车的速度;
(3)根据题意得出函数关系式即可;
(4)设B车行驶a小时可以追上A车,由追击问题的等量关系建立方程求出其解;
(1)由函数图象,得
l2表示乙车离出发地的距离y与追赶时间x之间的关系;
(2)甲车的速度为![]() =60km/h,乙车的速度为
=60km/h,乙车的速度为![]() =90km/h;
=90km/h;
(3)甲车的函数的关系式为:y1=60x+60;
乙车的函数关系式为:y2=90x;
(4)设乙车行驶a小时可以追上甲车,由题意,得
90a=60+60a,
解得:a=2,
∵1.5<2,
∴乙车不能在1.5小时内追上甲车,乙车追上甲车时,乙车行驶了2小时.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣![]() )×(﹣90)÷
)×(﹣90)÷![]()
(3)﹣2.5÷![]() ×(﹣
×(﹣![]() );
);
(4)(﹣10)2﹣[16+(﹣3)2]
(5)(![]() ﹣
﹣![]() +2)÷
+2)÷![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )
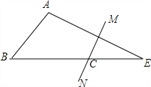
A. 45° B. 60° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1 , S2 , 当BD=1时,则S2﹣S1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC. 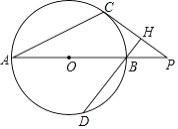
(1)求证:PC是⊙O的切线;
(2)若sin∠P= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com