
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )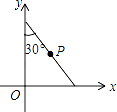
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
【答案】B
【解析】如图连接OP,因为![]() AOB=90°,
AOB=90°,![]() OAB=30°,
OAB=30°,
则![]() ABO=60°,
ABO=60°,
因为P是AB的中点,
所以OP=![]() AB=2,且OP=PB,
AB=2,且OP=PB,
则三角形OPB是等边三角形,
所以∠POB=60°,
因为现将此三角板绕点O顺时针旋转120°,
则点P也绕点O顺时针旋转120°到P'
则![]() COP'=
COP'=![]() POP'-
POP'-![]() POB=120°-60°=60°,
POB=120°-60°=60°,
又因为OP=OP',连接PP'交OB于C,则![]() OPP'=
OPP'=![]() OP'P=30°,则PP'
OP'P=30°,则PP'![]() OB,则OC=
OB,则OC=![]() OP'=1,CP'=
OP'=1,CP'=![]() OP’=
OP’=![]() ,
,
则P'(1,![]() ).故选B.
).故选B.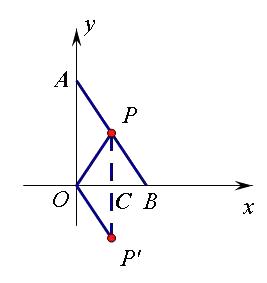
【考点精析】利用含30度角的直角三角形和直角三角形斜边上的中线对题目进行判断即可得到答案,需要熟知在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
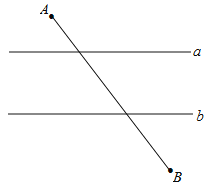
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下述命题中,真命题有( )
(1)对角线互相垂直的四边形是菱形
(2)三个角的度数之比为1:3:4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: ![]() :2的三角形是直角三角形.
:2的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线y= ![]() x交AB于点D,点P是直线y=
x交AB于点D,点P是直线y= ![]() x位于第一象限上的一点,连接PA,以PA为半径作⊙P,
x位于第一象限上的一点,连接PA,以PA为半径作⊙P, 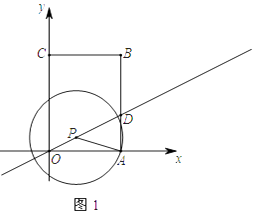
(1)连接AC,当点P落在AC上时,求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m, ①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线y= ![]() x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足 ![]() <
< ![]() <3时,求m的取值范围.(请直接写出答案)
<3时,求m的取值范围.(请直接写出答案)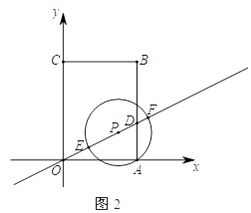
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C,D分别是BO,BA的中点,点E在CD的延长线上.若函数y1= ![]() (x>0)的图象经过B,E,函数y2=
(x>0)的图象经过B,E,函数y2= ![]() (x>0)的图象过点C,且△BCE的面积为1,则k2的值为( )
(x>0)的图象过点C,且△BCE的面积为1,则k2的值为( ) 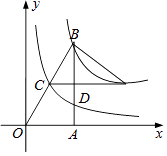
A.![]()
B.![]()
C.3
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线y=﹣ ![]() x+
x+ ![]() 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B. 
(1)求⊙A的半径;
(2)连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.
(3)如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分): 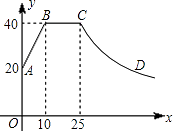
(1)上课后第5min与第30min相比较,何时学生注意力更集中?
(2)某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com