
【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线y= ![]() x交AB于点D,点P是直线y=
x交AB于点D,点P是直线y= ![]() x位于第一象限上的一点,连接PA,以PA为半径作⊙P,
x位于第一象限上的一点,连接PA,以PA为半径作⊙P, 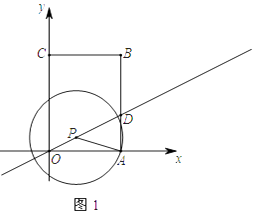
(1)连接AC,当点P落在AC上时,求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m, ①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线y= ![]() x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足 ![]() <
< ![]() <3时,求m的取值范围.(请直接写出答案)
<3时,求m的取值范围.(请直接写出答案)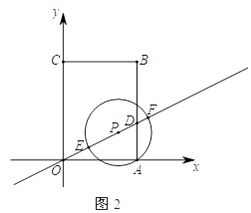
【答案】
(1)解:如图1中,

∵B(3,4)∴BC=3,AB=4
∵∠B=90°∴AC=5
∵OC∥AB,
∴△OPC∽△ADP,
∴ ![]() ,
,
即 ![]()
∴ ![]() .
.
(2)解:∵⊙P经过点O,
∴OP=AP
∴∠POA=∠PAO,
∵∠PDA+∠POA=∠DAP+∠PAO,
∴∠PDA=∠DAP,
∴△PAD是等腰三角形.
(3)解:①分4种情形讨论:
ⅰ)如图2中,
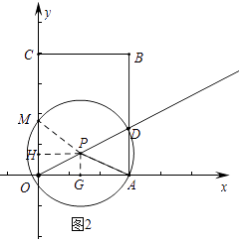
交点M是OC中点,PM=PA
则 ![]() ,
,
解得 ![]() .
.
ⅱ)如图3中,
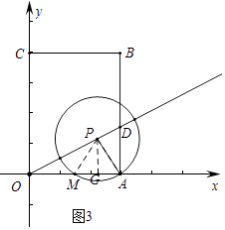
交点M是OA中点,PM=PA
∴MG=GA= ![]() ,
,
∴ ![]() .
.
ⅲ)如图4中,

交点M是AB中点,PM=PA
∴PG= ![]() AM=1,
AM=1,
∴PH=2DH=2× ![]() =1,
=1,
∴m=2.
ⅳ)如图5中,
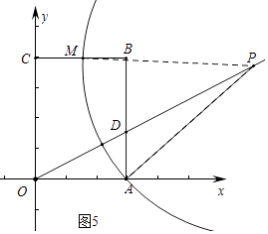
交点M是BC中点,PM=PA
则 ![]() ,
,
解得 ![]() .
.
综上所述,满足要求的m值为 ![]() 或
或 ![]() 或2或
或2或 ![]() .
.
②如图6中,当DE=3DF时,易知PA=2PD.

设P(m, ![]() ),则
),则 ![]() =2
=2 ![]() ,
,
解得m= ![]() 或4,
或4,
当m=4时,ED= ![]() DF,
DF,
综上可知,当DE,DF满足 ![]() <
< ![]() <3时,m的取值范围为
<3时,m的取值范围为 ![]() <m<4.
<m<4.
【解析】(1)由△OPC∽△ADP,可得 ![]() ,求出AC、AD即可解决问题;(2)只要证明∠PDA=∠DAP即可.(3)①分三种情形分别求解即可ⅰ)如图2中,交点M是OC中点,PM=PA;ⅱ)如图3中,交点M是OA中点,PM=PA;ⅲ)如图4中,交点M是AB中点,PM=PA;ⅳ)如图5中,交点M是BC中点,PM=PA;②如图6中,当DE=3DF时,易知PA=2PD.由此列出方程即可解决问题.
,求出AC、AD即可解决问题;(2)只要证明∠PDA=∠DAP即可.(3)①分三种情形分别求解即可ⅰ)如图2中,交点M是OC中点,PM=PA;ⅱ)如图3中,交点M是OA中点,PM=PA;ⅲ)如图4中,交点M是AB中点,PM=PA;ⅳ)如图5中,交点M是BC中点,PM=PA;②如图6中,当DE=3DF时,易知PA=2PD.由此列出方程即可解决问题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位) 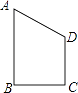
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点P是∠AOB的边OB上的一点(请利用网格作图,保留作图痕迹). 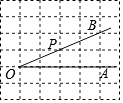
(1)过点P画OB的垂线,交OA于点C;
(2)线段的长度是点O到PC的距离;
(3)PC<OC的理由是;
(4)过点C画OB的平行线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )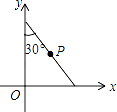
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答下列问题.
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.
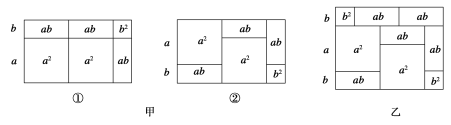
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元?
(2)若体育老师带了6000元去购买这种篮球与足球共80个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE. 
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com