
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
【答案】(1)见解析(2)①1;②2
【解析】
试题(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;
(2)①有(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形即∠DMA=90°,所以AM=![]() AD=1时即可;
AD=1时即可;
②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.
试题解析:(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵AM=1=![]() AD,
AD,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少元?
(2)若该商店A种纪念品每件售价24元,B种纪念品每件售价35元,这两种纪念品共购进1 000件,这两种纪念品全部售出后总获利不低于4 900元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)点 E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
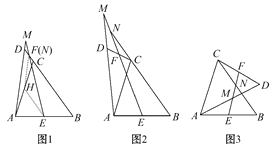
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
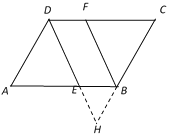
【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com