
【题目】关于x的方程 ![]() 的解为非正数,且关于x的不等式组
的解为非正数,且关于x的不等式组 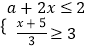 无解,那么满足条件的所有整数a的和是( )
无解,那么满足条件的所有整数a的和是( )
A.﹣19
B.﹣15
C.﹣13
D.﹣9
【答案】C
【解析】解:分式方程去分母得:ax﹣x﹣1=2,
整理得:(a﹣1)x=3,
由分式方程的解为非正数,得到 ![]() ≤0,且
≤0,且 ![]() ≠﹣1,
≠﹣1,
解得:a<1且a≠﹣2,
不等式组整理得:  ,
,
由不等式组无解,得到 ![]() <4,
<4,
解得:a>﹣6,
∴满足题意a的范围为﹣6<a<1,且a≠﹣2,即整数a的值为﹣5,﹣4,﹣3,﹣1,0,
则满足条件的所有整数a的和是﹣13,
所以答案是:C
【考点精析】通过灵活运用分式方程的解和一元一次不等式的解法,掌握分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
在上学期的学习中,我们知道若![]() ,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于
,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于![]() ,规定[a,m]=n,例如:
,规定[a,m]=n,例如:![]() ,所以[6,36]=2.
,所以[6,36]=2.
(1)根据上述规定,填空:[3,______]= 4,[2,32]=_____,[-4,1]=______,[5,0.2]=______;
(2)记![]() ,
,![]() ,求y与x之间的关系式.
,求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
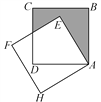
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2 020次变换后,正方形ABCD的对角线交点M的坐标变为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
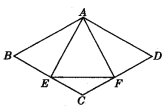
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往
两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往![]() 两地,如果从A市运往
两地,如果从A市运往![]() 两地运价分别为20元/吨和25元/吨,从B市运往
两地运价分别为20元/吨和25元/吨,从B市运往![]() 两地运价分别为15元/吨和22元/吨。
两地运价分别为15元/吨和22元/吨。
(1)如果A市运往C地的化肥为100吨,则总运费共多少元?
(2)设总运费为![]() 元,如果设A市运往C地的化肥
元,如果设A市运往C地的化肥![]() 吨,用含
吨,用含![]() 代数式来表示
代数式来表示![]() ;
;
(3)按照(2)问的要求,猜想![]() 为多少时,总的运费最少,是多少?
为多少时,总的运费最少,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的 ![]() ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降 ![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com