
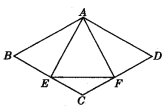
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
【答案】(1)见详解;(2)见详解
【解析】
(1)由菱形的性质可得AB=AD,∠B=∠D,又知BE=DF,所以利用SAS判定△ABE≌△ADF从而得到AE=AF;
(2)连接AC,由已知可知△ABC为等边三角形,已知E是BC的中点,则∠BAE=∠DAF=30°,即∠EAF=60°.因为AE=AF,所以△AEF为等边三角形.
(1)由菱形ABCD可知:
AB=AD,∠B=∠D,
∵BE=DF,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)连接AC,
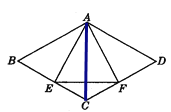
∵菱形ABCD,∠B=60°,
∴△ABC为等边三角形,∠BAD=120°,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一的性质),
∴∠BAE=30°,同理∠DAF=30°,
∴∠EAF=60°,由(1)可知AE=AF,
∴△AEF为等边三角形.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少元?
(2)若该商店A种纪念品每件售价24元,B种纪念品每件售价35元,这两种纪念品共购进1 000件,这两种纪念品全部售出后总获利不低于4 900元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
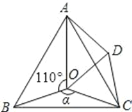
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园,图中描述了小丽路上的情景,下列说法中正确的是_______.
①小丽在便利店停留时间为15分钟
②公园离小丽家的距离为2000米
③小丽从家到达公园共用时间20分钟
④小丽从家到便利店的平均速度为100米/分钟

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com