
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
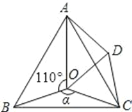
【答案】(1)见解析;(2)见解析;(3) 110°或125°或140°.
【解析】
(1)根据△BOC绕点C按顺时针方向旋转60°得△ADC,得CO=CD,∠OCD=60°故△COD是等边三角形;(2)求得∠ADO=∠ADC-∠CDO=90°即可知△AOD是直角三角形;(3)分别求出∠ADO=α-60°,∠AOD=360°-60°-110°-α=190°-α,再根据等腰三角形的底角相同分3中情况讨论.
解:(1)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC-∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α-60°,∠AOD=360°-60°-110°-α=190°-α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
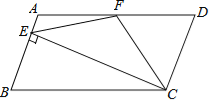
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
在上学期的学习中,我们知道若![]() ,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于
,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于![]() ,规定[a,m]=n,例如:
,规定[a,m]=n,例如:![]() ,所以[6,36]=2.
,所以[6,36]=2.
(1)根据上述规定,填空:[3,______]= 4,[2,32]=_____,[-4,1]=______,[5,0.2]=______;
(2)记![]() ,
,![]() ,求y与x之间的关系式.
,求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2 020次变换后,正方形ABCD的对角线交点M的坐标变为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
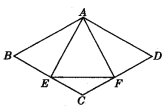
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy![]() ),其中x=2,y=-1。
),其中x=2,y=-1。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往
两地各需220吨和280吨化肥,A市有化肥200吨,B市有化肥300吨,刚好可以全部运往![]() 两地,如果从A市运往
两地,如果从A市运往![]() 两地运价分别为20元/吨和25元/吨,从B市运往
两地运价分别为20元/吨和25元/吨,从B市运往![]() 两地运价分别为15元/吨和22元/吨。
两地运价分别为15元/吨和22元/吨。
(1)如果A市运往C地的化肥为100吨,则总运费共多少元?
(2)设总运费为![]() 元,如果设A市运往C地的化肥
元,如果设A市运往C地的化肥![]() 吨,用含
吨,用含![]() 代数式来表示
代数式来表示![]() ;
;
(3)按照(2)问的要求,猜想![]() 为多少时,总的运费最少,是多少?
为多少时,总的运费最少,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家面临倒闭的企业在“调整产业结构,转变经营机制”的改革后,扭亏为盈. 下表是该企业2015年8~12月、2016年第一季度的月利润统计表:

根据以上信息,解答下列问题:
(1)2015年8月至2016年1月该企业利润的月平均利润为____万元,月利润的中位数为_____万元;
(2)已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com