
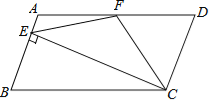
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
【答案】①②④
【解析】
试题解析:①∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,故此选项正确;
∠BCD,故此选项正确;
延长EF,交CD延长线于M,
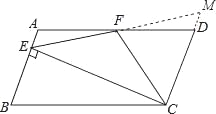
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
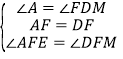 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少元?
(2)若该商店A种纪念品每件售价24元,B种纪念品每件售价35元,这两种纪念品共购进1 000件,这两种纪念品全部售出后总获利不低于4 900元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
, OA=10,E为x轴负半轴上一点,且tan∠AOE= ![]() .
.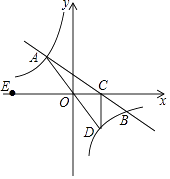
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)点 E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
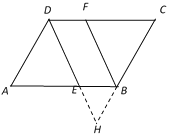
【题目】如图,直线AD∥BC,E,F分别在线段AB,CD上,∠ADE=∠FBC,判断直线DE与BF的位置关系,以下是解答过程,请补充完整,其中括号里填依据.
解:DE∥BF.
理由如下:延长DE交CB延长线于H点,
因为AD∥BC(__________).
所以∠ADE=∠H(__________).
又因为∠ADE=∠FBC(已知),
所以______=______(________).
所以DE∥BF(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
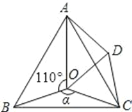
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com