
【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
(1)当AC=8,BC=6时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
![]()
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
(1)求证:OE=OF;
(2)连结DE、BF,试说明四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向向右平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 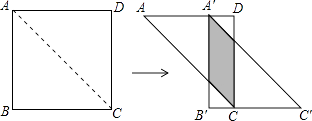
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生参加课外体育活动的情况,随机抽取了30名学生,对他们一周内平均每天参加课外体育活动的时间进行了调查,统计结果如下(单位:分):
28,50,40,40,40,53,38,40,34,40,27,21,35,32,40,
40,30,52,35,62,36,15,51,40,38,19,40,40,32,43.
(1)求这组数据的极差;
(2)按组距10分将数据分组,确定每组的组中值,列出频数分布表;
(3)在同一图中画出频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 是
是![]() 边上的一点,按要求画图,并保留作图痕迹.
边上的一点,按要求画图,并保留作图痕迹.
(1)用尺规作图法在![]() 的右侧以点
的右侧以点![]() 为顶点作
为顶点作![]() ;
;
(2)射线![]() 与
与![]() 的位置关系是____________,理由是____________.
的位置关系是____________,理由是____________.
(3)画出表示点![]() 到
到![]() 的距离的线段和表示点
的距离的线段和表示点![]() 到
到![]() 的距离的线段.
的距离的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.

(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
(2)若DC=2,求证:△ABD≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
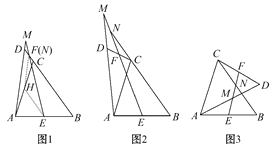
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com