练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

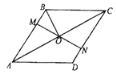
    【题目】如图，在菱形ABCD中，点M、 N分别在AB、CD上，AM=CN, MN与AC交于点O,连接BO,若∠BAC=29°，则∠OBC为________.

    【答案】61°

    【解析】

    由△AMO≌△CNO，推出AO=CO，由AB=CB，推出BO⊥AC，推出∠BOC=90°，∠BAC=29°，推出∠BCA=29°即可解决问题；

    ∵四边形ABCD为菱形，
    ∴AB∥CD，AB=BC，
    ∴∠MAO=∠NCO，∠AMO=∠CNO，
    在△AMO和△CNO中，

    ，
    ∴△AMO≌△CNO，
    ∴AO=CO，
    ∵AB=CB，
    ∴BO⊥AC，
    ∴∠BOC=90°，
    ∵∠BAC=29°，BA=BC，
    ∴∠BCA=∠BAC=29°，
    ∴∠OBC=90°-29°=61°．
    故答案是：61°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，

    ，

    ，……

    （1）依据上述规律，请写出=__________=______

    （2）当n为正整数时（n≥2），=_________________=_____________

    （3）计算的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    平均成绩

    中位数

    甲

    10

    8

    9

    8

    10

    9

    9

    ①

    乙

    10

    7

    10

    10

    9

    8

    ②

    9.5

    （1）完成表中填空①　 　；②　 　；

    （2）请计算甲六次测试成绩的方差；

    （3）若乙六次测试成绩方差为，你认为推荐谁参加比赛更合适，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 阅读下面的材料

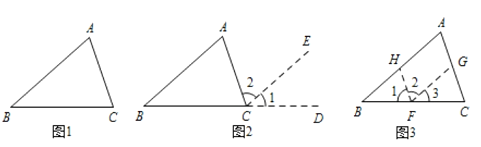
    图1，在△ABC中，试说明∠A+∠B+∠C=180°

    通过画平行线，将∠A、∠B、∠C作等量代换，使各角之和恰为一个平角，依辅助线不同而得多种方法：

    解：如图2，延长BC到点D，过点C作CE∥BA

    因为BA∥CE（作图所知）

    所以∠B=∠2，∠A=∠1（两直线平行，同位角、内错角相等）

    又因为∠BCD=∠BCA+∠2+∠1=180°（平角的定义）

    所以∠A+∠B+∠ACB=180°（等量代换）

    （1）如图3，过BC上任一点F，作FH∥AC，FG∥AB，这种添加辅助线的方法能说∠A+∠B+∠C=180°吗？并说明理由．

    （2）还可以过点A作直线MN∥BC，或在三角形内取点P过P作三边的平行线，请选择一种方法，画出相应图形，并说明∠A+∠B+∠C=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，陈老师对我们说，如果1条线段将一个三角形分成2个等腰三角形，那么这1条线段就称为这个三角形的“好线”，如果2条线段将一个三角形分成3个等腰三角形，那么这2条线段就称为这个三角形的“好好线”．

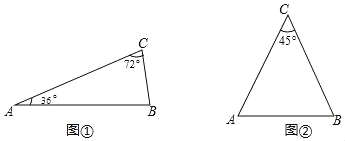
    (1)如图①，在△ABC中，∠A＝36°，∠C＝72°，请你在这个三角形中画出它的“好线”，并标出等腰三角形顶角的度数．

    (2)如图②，已知△ABC是一个顶角为45°的等腰三角形，请你在这个三角形中画出它的“好好线”，并标出所分得的等腰三角形底角的度数．

    （应用）

    (3)在△ABC中，已知一个内角为42°，若它只有“好线”，请你写出这个三角形最大内角的度数：___ ___ （写出其中两种情形即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是直线AB上一点，OD平分∠BOC，∠COE＝90°.

    (1)若∠AOC＝36°，求∠DOE的度数；

    (2)若∠AOC＝α，则∠DOE＝________.(用含α的代数式表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

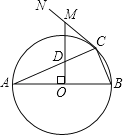
    【题目】如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．

    （1）求证：MD=MC；

    （2）若⊙O的半径为5，AC=4，求MC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲骑自行车从M地出发沿一条公路匀速前往N地，乙骑摩托车从N地出发沿同一条公路匀速前往M地，

    已知乙比甲晚出发0.5小时且先到达目的地．设甲行驶的时间为t(h)，甲乙两人之间的路程为y(km)，

    y与t的函数关系如图1所示，请解决以下问题：

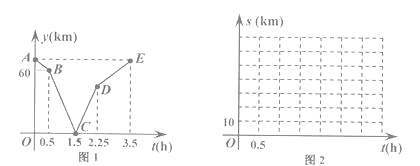
    （1）写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式．

    （2）①求点D的纵坐标．

    ②求M，N两地之间的距离．

    （3）设乙离M地的路程为S乙 (km)，请直接写出S甲 与时间t(h)的函数表达式，并在图2所给的直角坐标系中画出它的图象．

    查看答案和解析>>

    同步练习册答案