
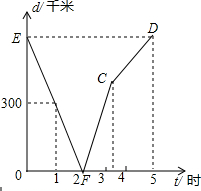
 甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象.
甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象.分析 (1)观察函数图象,发现当d=0时,t=2,即2小时两车相遇;
(2)由函数图象可知甲车5小时到达B城,根据“速度=路程÷时间”即可求出甲车的速度,再根据两车2小时相遇可算出两车的速度和,用两车速度和减去甲车速度即可得出乙车的速度;
(3)由甲车从A城出发,结合“距离=甲车速度×时间”即可得出s甲关于x的函数解析式;由乙车从B城出发,结合“距离=两地距离-乙车速度×时间”即可得出s乙关于x的函数解析式;
(4)根据“行驶时间=两车行驶的路程÷两车的速度和”结合两车行驶的过程,即可得出结论.
解答 解:(1)观察函数图象可以发现:
当t=1时,d=300,而t=2时,d=0,
∴当t=0时,d=2×(300-0)=600.
∴A、B两地相距600千米.
当d=0时,t=2,
∴经过2小时两车相遇.
故答案为:600,2.
(2)甲车的速度为:600÷5=120(千米/时);
乙车的速度为:600÷2-120=180(千米/时).
答:甲车的速度为120千米/时,乙车的速度为180千米/时.
(3)结合题意可知:s甲=120x,
s乙=600-180x.
(4)两车第一次相距100千米的时间为:(600-100)÷(180+120)=$\frac{5}{3}$(小时);
两车第二次相距100千米的时间为:(600+100)÷(180+120)=$\frac{7}{3}$(小时).
∵180×$\frac{7}{3}$=420(千米),420<600,
∴第二次相距100千米时,乙车尚未到达终点,该时间符合题意.
答:当两车相距100千米路程时,t的值为$\frac{5}{3}$小时或$\frac{7}{3}$小时.
点评 本题考查了一次函数的应用以及一次函数的图象,属于基础题,难度不大,解决该题型题目时,根据数量关系列出算式(或函数关系式)是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | -3-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -t2的系数是-1 | B. | -$\frac{2mn}{3}$的系数是-$\frac{2}{3}$ | ||
| C. | xy2的系数是1 | D. | 3πa2的系数是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com