
 已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点
已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点分析 (1)对于直线解析式,令x与y为0,分别求出y与x的值,确定出A与B的坐标即可;
(2)过点D作DH⊥x轴于H,DG⊥y轴于G,由D与A的坐标确定出DG与AG的长,利用勾股定理求出AD的长,再求出AB与BD的长,利用勾股定理的逆定理判断即可得证;
(3)作出线段AD的垂直平分线,交x轴于点C,连接AC,DC,利用垂直平分线定理得到AC=DC,设C坐标为(x,0),利用两点间的距离公式列出关于x的方程,求出方程的解得到x的值,即可确定出C的坐标.
解答 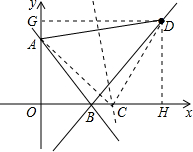 解:(1)对于直线解析式y=-$\frac{4}{3}$x+4,
解:(1)对于直线解析式y=-$\frac{4}{3}$x+4,
令x=0,得到y=4,令y=0,得到x=3,
则A(0,4),B(3,0);
(2)过点D作DH⊥x轴于H,DG⊥y轴于G,
∵D(11,6),A(0,4),
∴DG=11,AG=2,
由勾股定理得:AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=$\sqrt{125}$,
∵AB2=42+32=25,BD2=82+62=100,
∴AB2+BD2=AD2,
则△ABD是直角三角形;
(3)作AD的垂直平分线,交x轴于点C,连接AC,DC,此时AC=DC,
设OC长为x,由两点间的距离公式得:x2+42=(11-x)2+62,
解得:x=$\frac{141}{22}$,
则C($\frac{141}{22}$,0).
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,勾股定理,勾股定理的逆定理,以及等腰三角形的性质,熟练掌握定理及性质是解本题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
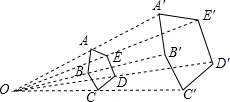 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形,A′B′C′D′E′,已知OA=10cm,OA′=20cm,五边形ABCDE的周长为15cm,则五边形A′B′C′D′E′的周长为30cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
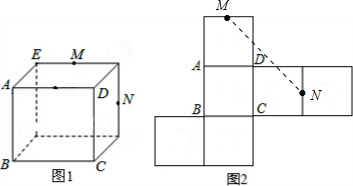 图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )
图1为一个长方体,AD=AB=10,AE=6,M,N为所在棱的中点,图2为图1的表面展开图,则图2中MN的长度为( )| A. | 11$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 10 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
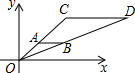 如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )
如图,在直角坐标系中,△OAB和△OCD是位似图形,O为位似中心,若A点的坐标为(1,1),B点的坐标为(2,1),C点的坐标为(3,3),那么点D的坐标是( )| A. | (4,2) | B. | (6,3) | C. | (8,4) | D. | (8,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com