
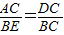 ;
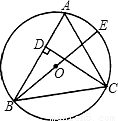
;
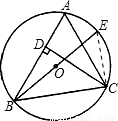 (1)证明:连接EC,
(1)证明:连接EC,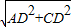 =3
=3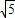 ,
,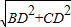 =10,
=10,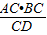 =5
=5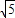 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2006•凉山州)如图所示,分别按A、B两种方法用钢丝绳捆扎圆形钢管的截面图:设A、B两种方法捆扎所需的绳子的长分别为a、b(不计接头部分),则a、b的大小关系为:a
(2006•凉山州)如图所示,分别按A、B两种方法用钢丝绳捆扎圆形钢管的截面图:设A、B两种方法捆扎所需的绳子的长分别为a、b(不计接头部分),则a、b的大小关系为:a查看答案和解析>>
科目:初中数学 来源:2011年山东省中考数学模拟试卷(三)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《一次函数》(07)(解析版) 题型:解答题
 +8与x轴、y轴分别交于A、B两点,M为OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的B′处,则直线AM的解析式为______.
+8与x轴、y轴分别交于A、B两点,M为OB上一点,若将△ABM沿AM折叠,点B恰好落在x轴上的B′处,则直线AM的解析式为______.
查看答案和解析>>
科目:初中数学 来源:2010年山东省青岛市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年四川省凉山州中考数学试卷(大纲卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com