
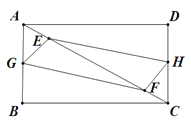
����Ŀ���ı���ABCD �У�AB=3��BC=4��E��F �ǶԽ��� AC�ϵ��������㣬�ֱ�� A��C ͬʱ������ ������У��ٶȾ�Ϊ 1cm/s���˶�ʱ��Ϊ t �룬������һ�����㵽����ֹͣ�˶���
��1���� G��H �ֱ��� AB��DC �е㣬��֤���ı��� EGFH ʼ����ƽ���ı��Σ�
��2���ڣ�1�������£��� t Ϊ��ֵʱ���ı��� EGFH Ϊ���Σ�
��3���� G��H �ֱ������� A��B��C��C��D��A �ϵĶ��㣬�� E��F ��ͬ���ٶ�ͬʱ�������� t Ϊ��ֵʱ���ı��� EGFH Ϊ���Σ�
���𰸡���1��֤����������
��2���� t Ϊ0.5s��4.5sʱ���ı��� EGFH Ϊ���Σ�
��3��tΪ![]() sʱ���ı���EGFHΪ����.
sʱ���ı���EGFHΪ����.
�������������������1���ɾ��ε����ʵó�AB=CD��AB��CD��AD��BC����B=90�㣬�ɹ��ɶ������AC=5����SAS֤����AFG�ա�CEH���ó�GF=HE��ͬ���ó�GE=HF�����ɵó����ۣ�
��2����֤���ı���BCHG��ƽ���ı��Σ��ó�GH=BC=4�����Խ���EF=GH=4ʱ��ƽ���ı���EGFH�Ǿ��Σ��������������AE=CF=t���ó�EF=5-2t=4���ⷽ�̼��ɣ���AE=CF=t���ó�EF=5-2��5-t��=4���ⷽ�̼��ɣ�
��3������AG��CH�������ε����ʵó�GH��EF��OG=OH��OE=OF���ó�OA=OC��AG=AH��֤���ı���AGCH�����Σ��ó�AG=CG����AG=CG=x����BG=4-x���ɹ��ɶ����ó����̣��ⷽ�����BG���ó�AB+BG=![]() �����ɵó�t��ֵ��
�����ɵó�t��ֵ��
�����������1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AB��CD��AD��BC����B=90����
��AC=![]() =5����GAF=��HCE��
=5����GAF=��HCE��
��G��H�ֱ���AB��DC�е㣬
��AG=BG��CH=DH��
��AG=CH��
��AE=CF��
����AFG����CEH��
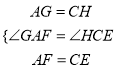
���AFG�ա�CEH��SAS����
��GF=HE��
ͬ����GE=HF��
���ı���EGFH��ƽ���ı��Σ�
��2���ɣ�1���ã�BG=CH��BG��CH��
���ı���BCHG��ƽ���ı��Σ�
��GH=BC=4����EF=GH=4ʱ��ƽ���ı���EGFH�Ǿ��Σ������������
��AE=CF=t��EF=5��2t=4����ã�t=0.5��
��AE=CF=t��EF=5��2��5��t��=4����ã�t=4.5��
������������tΪ0.5s��4.5sʱ���ı���EGFHΪ���Σ�
��3������AG��CH����ͼ��ʾ��
���ı���EGFHΪ���Σ�
��GH��EF��OG=OH��OE=OF��
��OA=OC��AG=AH��
���ı���AGCH�����Σ�
��AG=CG��
��AG=CG=x����BG=4��x���ɹ��ɶ����ã�AB2+BG2=AG2����32+��4��x��2=x2��
��ã�x=![]() ��
��
��BG=4��![]() =
=![]() ��
��
��AB+BG=3+![]() =
=![]() ��
��
��tΪ![]() sʱ���ı���EGFHΪ���Σ�
sʱ���ı���EGFHΪ���Σ�


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��������У����Ϊ�������ǣ�������
A. ������3�� B. ����3��������2�� C. ������2��3 D. ��|��3|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ����ÿ������������������¼�¼���±���
���� | һ | �� | �� | �� | �� | �� | �� |
������� | 10�� | 12�� | 11�� | 9�� | 7�� | 5�� | 7�� |
������� | 2�� | 1�� | 0�� | ��1�� | ��4�� | ��5�� | ��5�� |
���²�����һ��������_____����һ���²�Ϊ_____�森
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
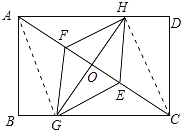
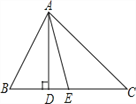
����Ŀ����ͼ���ڡ�ABC�У���B=65���C=45�㣬AD��BC���ϵĸߣ�AE�ǡ�BAC��ƽ�ߣ����DAE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
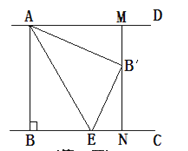
����Ŀ����ͼ����֪AD��BC��AB��BC��AB=3. ��EΪ����BC��һ�����㣬����AE������ABE��AE�۵�����B���ڵ�B����������B����AD�Ĵ��ߣ��ֱ�AD��BC�ڵ�M��N. ����B��Ϊ�߶�MN�����ȷֵ�ʱ��BE�ij�Ϊ__________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.����ֱ��
B.ƽ���ҵ�ֱ����ֱ��
C.������ȵ��������ǵȻ�
D.Բ�ĶԳ����������������Գ�����ֻ��һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
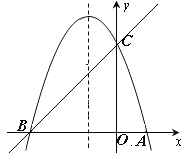
��ͼ����֪������y��ax2��bx��c(a��0)�ĶԳ���Ϊֱ��x����1���Ҿ���A��1��0����C��0��3�����㣬��x�����һ������ΪB.
����ֱ��y��mx��n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
���������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�����M�����ꣻ�����PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
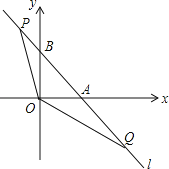
����Ŀ����ͼ��ֱ��l��y=��x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
��1�����AOB���ܳ���
��2����AQ=t��0�����ú�t�Ĵ���ʽ��ʾ��P�����ꣻ
��3��������P��Q��ֱ��l���˶���ʹ�á�AOQ���BPO���ܳ����ʱ����tan��AOQ=m��������A�Ķ��κ���y=ax2+bx+cͬʱ������������������
��6a+3b+2c=0��
�ڵ�m��x��m+2ʱ������y�����ֵ����![]() ���������ϵ��a��ֵ��
���������ϵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨�������㡰������������������a��b���涨a��b��ab+a��b�����磺1��2��1��2+1��2��1�������3������6����_____
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com