
 小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.
小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.科目:初中数学 来源: 题型:
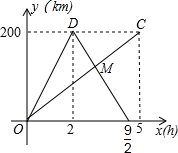 甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=60°,半径为2
如图,已知∠AOB=60°,半径为2| 3 |
| A、2 | B、2或6 |
| C、4或6 | D、1或5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
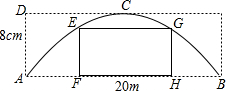 有一个抛物线形拱桥,其最大高度AD为8m,跨度AB为20m,为了对拱桥进行加固,需要在拱桥内安装矩形脚手架EFHG,已知脚手架的高EF为5m.
有一个抛物线形拱桥,其最大高度AD为8m,跨度AB为20m,为了对拱桥进行加固,需要在拱桥内安装矩形脚手架EFHG,已知脚手架的高EF为5m.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点O为圆心,正方形的对角线OB长为半径作弧,交x轴于点A.请根据图形填空.
我们在学习实数时,画了这样一个图:即以数轴上1个单位长的线段为边作正方形,再以原点O为圆心,正方形的对角线OB长为半径作弧,交x轴于点A.请根据图形填空.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com