
 如图,已知∠AOB=60°,半径为2
如图,已知∠AOB=60°,半径为2| 3 |
| A、2 | B、2或6 |
| C、4或6 | D、1或5 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
 解:当将⊙M水平向左平移,当点M运动到M′位置时,如图
解:当将⊙M水平向左平移,当点M运动到M′位置时,如图| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| EM′2-EH2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| MQ | ||
|
| 3 |
| 3 |
| 3 |
| M″D | ||
|
| 3 |
| MC | ||
|


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
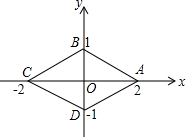 如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是查看答案和解析>>
科目:初中数学 来源: 题型:
 小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.
小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )
如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )| A、26cm2 |
| B、39cm2 |
| C、13cm2 |
| D、52cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com