
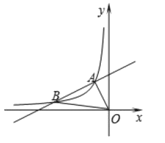
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、点
、点![]() ,在
,在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的周长最小,则点
的周长最小,则点![]() 的坐标是____________________________。
的坐标是____________________________。
【答案】![]()
【解析】
先根据点A求出k2值,再根据反比例函数解析式求出n值,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,设直线A′B的表达式为y=ax+c,根据待定系数法求得解析式,令y=0,即可求得P的坐标.
(1)∵反比例![]() 的图象经过点A(-1,2),
的图象经过点A(-1,2),
∴k2=-1×2=-2,
∴反比例函数表达式为:y=-![]() ,
,
∵反比例y=-![]() 的图象经过点B(-4,n),
的图象经过点B(-4,n),
∴-4n=-2,解得n=![]() ,
,
∴B点坐标为(-4,![]() ),
),
如图,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,
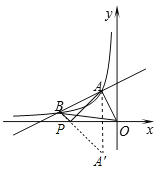
∵点A′和A(-1,2)关于x轴对称,
∴点A′的坐标为(-1,-2),
设直线A′B的表达式为y=ax+c,
∵经过点A′(-1,-2),点B(-4,![]() )
)
∴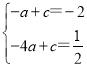 ,
,
解得: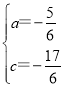 ,
,
∴直线A′B的表达式为:y=-![]() x-
x-![]() ,
,
当y=0时,则x=-![]() ,
,
∴P点坐标为(-![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=![]() ;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
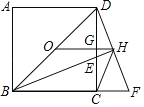
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段MN=a.
![]()
(1)求作:边长为![]() a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
(2)若a=10cm.求(1)中正三角形ABC的内切圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
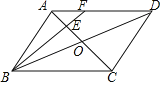
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与反比例函数在第三象限内的图象相交于点
,与反比例函数在第三象限内的图象相交于点![]() 。
。
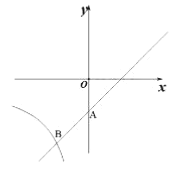
(1)求反比例函数的关系式;
(2)将直线![]() 沿
沿![]() 轴平移后与反比例函数图象在第三象限内交于点
轴平移后与反比例函数图象在第三象限内交于点![]() ,且
,且![]() 的面积为8,求平移后的直线的函数关系式。
的面积为8,求平移后的直线的函数关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
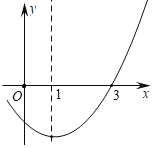
【题目】若二次函数y=x2﹣2x+k的部分图象如图所示,则关于x的一元二次方程x2﹣2x+k=0的解一个为x1=3,则方程x2﹣2x+k=0另一个解x2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com