
【题目】如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=![]() ;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
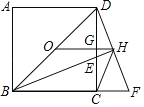
A.1B.2C.3D.4
【答案】D
【解析】
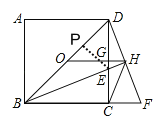
①过点E作EP⊥BD于点P,求出EC=CF,证明△BCE≌△DCF,然后可得BH⊥DF,再根据等腰三角形三线合一与中位线定理可得出结论;
②③由三角形中位线定理知,OG=![]() BC=
BC=![]() ,GH=
,GH=![]() CF=
CF=![]() ,然后可得结论;
,然后可得结论;
④根据四边形ABCD是正方形,BE是∠DBC的平分线可求出∠EBC=22.5°,进而得到∠F=67.5°,再由H是DF中点,可得CH=HF,求出∠CHF即可得出结论;
⑤证明△HEC∽△HCB,则HC:HB=HE:HC,即CH2=HEHB,即可得到⑤正确.
解:①过点E作EP⊥BD于点P,则EP=EC,
∵∠BDC=45°,
∴PD=EP,
易证△BEP≌△BEC,
∴BP=BC,
∵BD=BF,
∴PD=CF,
∴EC=CF,
∵∠BCE=∠DCF,BC=DC,
∴△BCE≌△DCF(SAS),
∴∠CBE=∠CDF,
∵∠CBE+∠BEC=90°,∠BEC=∠DEH,
∴∠DEH+∠CDF=90°,
∴∠BHD=∠BHF=90°,即BH⊥DF,
∴DH=HF,
∵OD=OB,
∴OH是△DBF的中位线,
∴OH∥BF,故①正确;
②③∵点O为正方形ABCD的中心,AD=1,BD=BF,
∴BD=BF=![]() ,
,
由三角形中位线定理知,OG=![]() BC=
BC=![]() ,GH=
,GH=![]() CF=
CF=![]() ,
,
∴OG:GH=1:(![]() ﹣1),
﹣1),
故②错误,③正确;
④∵四边形ABCD是正方形,BE是∠DBC的平分线,
∴∠EBC=22.5°,
∵∠BHF=90°,
∴∠F=90°﹣22.5°=67.5°,
∵H是DF中点,
∴CH=HF,
∴∠CHF=180°﹣67.5°﹣67.5°=45°,
∴∠CHF=2∠EBC,故④正确;
⑤∵∠CHF=∠CDF+∠ECH=2∠EBC,∠EBC=∠CDF,
∴∠ECH=∠CBH,
∵∠CHE=CHB,
∴△HEC∽△HCB,
∴HC:HB=HE:HC,即CH2=HEHB,故⑤正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴的两个交点分别为A(1,0)、B(3,0),与y轴的交点为C.
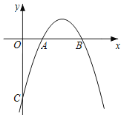
(1)求这个二次函数的表达式;
(2)在x轴上方的二次函数图象上,是否存在一点E使得以B、C、E为顶点的三角形的面积为![]() ?若存在,求出点E坐标;若不存在,请说明理由.
?若存在,求出点E坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
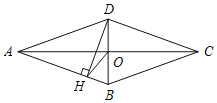
A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,三个顶点坐标分别为A(0,3)、B(3、4)、C(2,2)(网格中每个正方形的边长是1个单位长度).
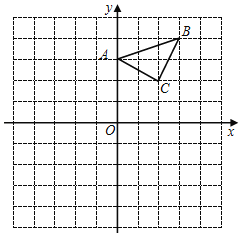
(1)以点B为位似中心,在网格内画出△A′BC′,使△A′BC′与△ABC位似,且位似比为2:1,则点C′的坐标是______;
(2)△A′BC′的面积是_______平方单位;
(3)在x轴上找出点P,使得点P到B与点A距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边AB上一点,延长AD至F使DF=BE,连接CF.
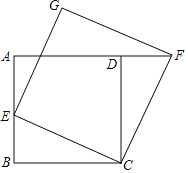
(1)求证:∠BCE=∠DCF;
(2)过点E作EG∥CF,过点F作FG∥CE,问四边形CEGF是什么特殊的四边形,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
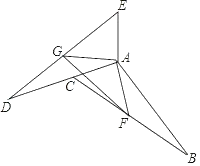
【题目】如图,把△ABC 绕点 A 顺时针旋转 n 度(0<n<180)后得到△ADE,并使点 D 落在 AC 的延长线上.
(1)若∠B=17°,∠E=55°,求 n;
(2)若 F 为 BC 的中点,G 为 DE 的中点,连 AG、AF、FG,求证:△AFG 为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结BE.
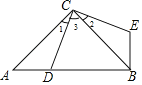
(1)求证:△ACD≌△BCE;
(2)当∠1=25°时,求∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
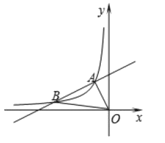
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、点
、点![]() ,在
,在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的周长最小,则点
的周长最小,则点![]() 的坐标是____________________________。
的坐标是____________________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com