
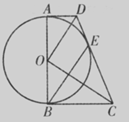
如图,在梯形ABCD中,AD∥BC,∠B=900,以AB为直径作⊙O,恰与另一腰CD相切于点E,连接OD、OC、BE.
(1)求证:OD∥BE;
(2)若梯形ABCD的面积是48,设OD=x,OC=y,且x+y=14,求CD的长.
(1)证明:连接OE,
∵CD是⊙O的切线, ∴OE⊥CD:)
在Rt△OAD和Rt△OED中,OA=OE, OD=OD,
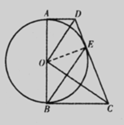 ∴Rt△OADcR≌t△OED, ∴∠AOD=∠EOD=
∴Rt△OADcR≌t△OED, ∴∠AOD=∠EOD=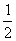 ∠AOE,
∠AOE,
在⊙O中,ABE=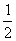 ∠AOE, ∴∠AOD=∠ABE,
∠AOE, ∴∠AOD=∠ABE,
∴OD∥BE
(2)同理可证:Rt△COE≌Rt△COB.∴∠COE=∠COB=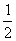 ∠BOE,
∠BOE,
∴∠DOE+∠COE=900,∴△COD是直角三角形,
∵S△DEO=S△DAO, S△COE=S△COB,
∴S梯形ABCD =2(S△DOE+S△COE)=2S△COD=OC·OD=48,即xy=48,
又∵x+y= 14,∴x2 +y2=(x+y)2-2xy=142-2×48=100,
在Rt△COD中,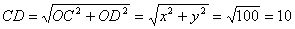
即CD的长为10.


科目:初中数学 来源: 题型:
如图,已知矩形ABCD的长AB为5,宽BC为4.E是BC边上的一个动点,
AE⊥上EF,EF交CD于点F.设BE=x,FC=y,则点 E从点B运动到点C时,
能表示y关于x的函数关系的大致图象是
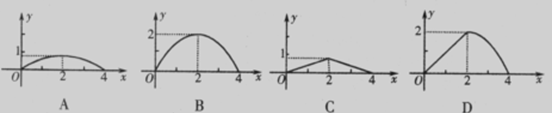
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,用红、蓝两种颜色随机地对A,B,C三个区域分别进行涂色,每个区域必须涂色并且只能涂一种颜色,请用列举法(画树状图或列表)求A,C两个区域所涂颜色不相同的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com