
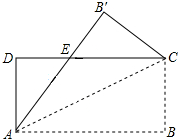
 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11. 分析 由四边形ABCD为矩形及折叠的特性,得到B′C=BC=AD,∠B′=∠B=∠D=90°,∠B′EC=∠DEA,得到△AED≌△CEB′,根据全等三角形的性质即可得到结论.
解答 解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA,
在△AED和△CEB′中,$\left\{\begin{array}{l}{∠B′EC=∠DEA}\\{∠B′=∠D}\\{B′C=AD}\end{array}\right.$,
∴△AED≌△CEB′(AAS),
∴DE=B′E,
∴△EB′C的周长=CE+B′E+B′C=CE+DE+AD=11,
故答案为:11.
点评 本题主要考查了图形的折叠问题,全等三角形的判定和性质,及矩形的性质.熟记翻折前后两个图形能够重合找出相等的角是解题的关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题
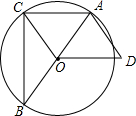 如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.
如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
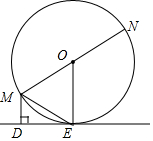 已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象与x轴有两个交点 | B. | 方程x2-2mx=3的两根之积为-3 | ||
| C. | 它的图象的对称轴在y轴的右侧 | D. | x<m时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
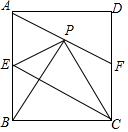 如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).
如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
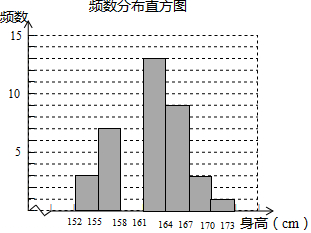 某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.| 身高分组 | 频数 | 频率 |
| 152≤x<155 | 3 | 0.06 |
| 155≤x<158 | 7 | 0.14 |
| 158≤x<161 | m | 0.28 |
| 161≤x<164 | 13 | n |
| 164≤x<167 | 9 | 0.18 |
| 167≤x<170 | 3 | 0.06 |
| 170≤x<173 | 1 | 0.02 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com