
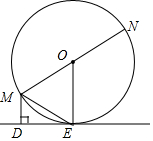
 已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.分析 (1)求出OE∥DM,求出OE⊥DE,根据切线的判定得出即可;
(2)连接EN,求出∠MDE=∠MEN,求出△MDE∽△MEN,根据相似三角形的判定得出即可.
解答 证明:(1)∵ME平分∠DMN,
∴∠OME=∠DME,
∵OM=OE,
∴∠OME=∠OEM,
∴∠DME=∠OEM,
∴OE∥DM,
∵DM⊥DE,
∴OE⊥DE,
∵OE过O,
∴DE是⊙O的切线;
(2)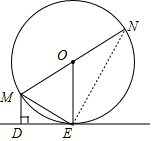
连接EN,
∵DM⊥DE,MN为⊙O的直径,
∴∠MDE=∠MEN=90°,
∵∠NME=∠DME,
∴△MDE∽△MEN,
∴$\frac{ME}{MD}$=$\frac{MN}{ME}$,
∴ME2=MD•MN
点评 本题考查了切线的判定,圆周角定理,相似三角形的性质和判定等知识点,能综合运用知识点进行推理是解此题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
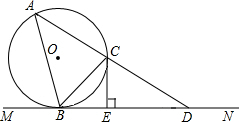 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1128 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
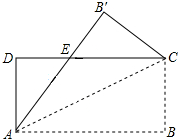 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )
某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )| A. | 40% | B. | 70% | C. | 76% | D. | 96% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com