
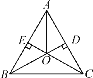
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,CE,BD相交于点O,则图中全等的直角三角形有__对.
【答案】4
【解析】
首先证明△ACE≌△ABD可得AD=AE,EC=BD,根据等式的性质可得AB-AE=AC-AD,即EB=DC;再证明△EBC≌△DCB,△EOB≌△DOC即可.
解:△ACE≌△ABD,△EBC≌△DCB,△EOB≌△DOC,
∵BD、CE为高,
∴∠ADB=∠AEC=,90°,
在△AEC和△ADB中,
∠A=∠A,∠AEC=∠ADB,AB=AC,
∴△ACE≌△ABD(ASA);
∴AD=AE,EC=BD,
∴AB-AE=AC-AD,
即EB=DC,
在△EBC和△DCB中,
EB=DC,BC=BC,EC=DB,∴△EBC≌△DCB(SSS),
在△EOB和△DOC中,
EB=DC,∠OEB=∠ODC,∠EOB=∠DOC,
∴△EOB≌△DOC(AAS).
故答案为:3.
“点睛”本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2 ![]() =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
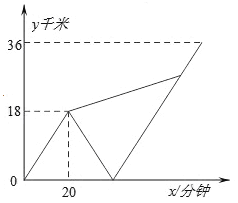
【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)电动车的速度为 千米/分钟;
(2)甲步行所用的时间为 分;
(3)求乙返回到学校时,甲与学校相距多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.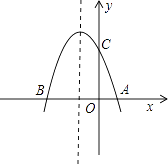
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c过点(2,﹣2)和(﹣1,10),与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长. 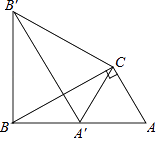
查看答案和解析>>
科目:初中数学 来源: 题型:
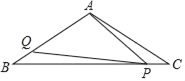
【题目】如图,已知△ABC中,AB=AC=![]() cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 . 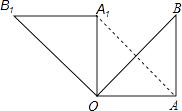
(1)线段OA1的长是 , ∠AOB1的度数是;
(2)连接AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求点B旋转到点B1的位置所经过的路线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com