
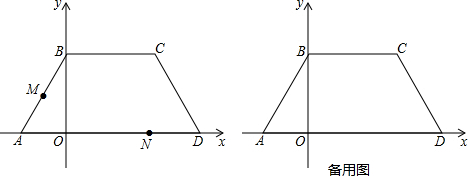
分析 (1)根据AB=BC=CD=2且点A(-1,0)得出OA=1,再根据勾股定理求出OB的长即可得出B点坐标,再由OD的长可得出D点坐标;
(2)当0≤t≤2时,根据锐角三角函数的定义得出M($\frac{t}{2}$-1,$\frac{\sqrt{3}}{2}$t),N(3-t,0),则以MN为直径的圆心O′(1-$\frac{t}{4}$,$\frac{\sqrt{3}t}{4}$),过O′作O′G⊥BC,交BC于点G,则G(1-$\frac{t}{4}$,$\sqrt{3}$),当以MN为直径的圆与直线BC相切,则O′G=$\frac{1}{2}$MN,再由两点间的距离公式即可得出t的值;当2<t≤4时,若以MN为直径的圆与直线BC相切,则MN⊥BC,BM=ON 即t-2=3-t,由此可得出t的值;
(3)当t=3时,M(1,$\sqrt{3}$).若∠DPO=∠DMO,则存在⊙Q,使得点O、D、P、M在⊙Q上,再由点Q在OD的垂直平分线上,可设Q($\frac{3}{2}$,n),根据QM=QO求出n的值,故可得出Q点的坐标,求出PQ的长,再分当点P在点Q上方与下方两种情况即可得出结论.
解答 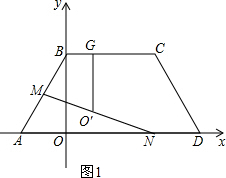 解:(1)∵AB=BC=CD=2且点A(-1,0)得出OA=1,
解:(1)∵AB=BC=CD=2且点A(-1,0)得出OA=1,
∴OB=$\sqrt{{AB}^{2}-{OA}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴B(0,$\sqrt{3}$).
∵梯形ABCD是等腰梯形,BC=2,OA=1,
∴OD=2+1=3,
∴D(3,0);
(2)分两种情况,
①如图1,当0≤t≤2时,
∵Rt△AOB中,∠AOB=90°,AO=$\frac{1}{2}$AB
∴∠BAO=60°,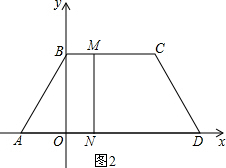
∴M($\frac{t}{2}$-1,$\frac{\sqrt{3}}{2}$t),N(3-t,0),
则以MN为直径的圆心O′(1-$\frac{t}{4}$,$\frac{\sqrt{3}t}{4}$),过O′作O′G⊥BC,交BC于点G
则G(1-$\frac{t}{4}$,$\sqrt{3}$),
法1,当以MN为直径的圆与直线BC相切,则O′G=$\frac{1}{2}$MN
∴$\sqrt{3}$-$\frac{\sqrt{3}t}{4}$=$\frac{1}{2}$$\sqrt{(4-\frac{3}{2}{t)}^{2}+(\frac{\sqrt{3}t}{2})^{2}}$即t1=t2=$\frac{4}{3}$,
法2:可用KMG-KNG=-1或构造相似或勾股定理等方法求出t.
②如图2,当2<t≤4时,
∵若以MN为直径的圆与直线BC相切,则MN⊥BC,
∴BM=ON 即t-2=3-t,
∴t=$\frac{5}{2}$.
综上,当t=$\frac{4}{3}$或t=$\frac{5}{2}$时,以MN为直径的圆与直线BC相切;
(3)存在.
如图3,当t=3时,M(1,$\sqrt{3}$).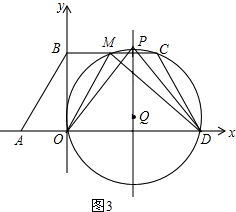
若∠DPO=∠DMO,则存在⊙Q,使得点O、D、P、M在⊙Q上,
又∵点Q在OD的垂直平分线上,可设Q($\frac{3}{2}$,n),
∴QM=QO即$\sqrt{\frac{1}{4}+(n-\sqrt{3})^{2}}$=$\sqrt{\frac{9}{4}+{n}^{2}}$,解得n=$\frac{\sqrt{3}}{6}$,即Q($\frac{3}{2}$,$\frac{\sqrt{3}}{6}$),
∴PQ=OQ=$\sqrt{\frac{9}{4}+\frac{3}{36}}$=$\frac{\sqrt{21}}{3}$;
①当点P在点Q上方时,yp=PQ+yQ=$\frac{\sqrt{3}}{6}$+$\frac{\sqrt{21}}{3}$;
②当点P在点Q下方时,
由对称性质,可得yp=PQ-yQ=$\frac{\sqrt{3}}{6}$-$\frac{\sqrt{21}}{3}$;
综上所述:点P的纵坐标为$\frac{\sqrt{3}}{6}$+$\frac{\sqrt{21}}{3}$或$\frac{\sqrt{3}}{6}$-$\frac{\sqrt{21}}{3}$.
点评 本题考查的是四边形综合题,涉及到勾股定理、切线的判定与性质、角平分线的性质等知识,在解答(2)、(3)时要注意分类讨论.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
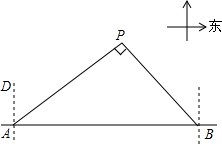 钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
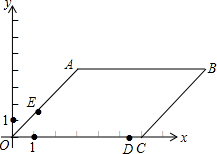 如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com