
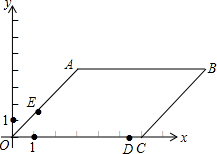
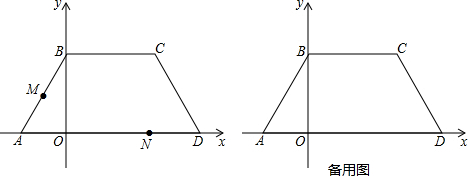
 如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)分析 (1)根据OC的长及B的坐标,确定出tan∠BCX的值,即为tan∠AOC的值;
(2)根据题意得到ED过平行四边形的中心,列出关于t的方程,求出方程的解即可得到结果;
(3)由E与C的坐标,得到EC与y轴平行,确定出三角形BEC为直角三角形,分两种情况考虑:当P位于如图P2时,∠EBP2=90°;当P位于如图P1时,∠EP1B=90°,作P1G⊥AB,垂足为G,分别求出P的坐标即可.
解答 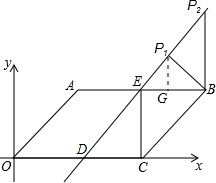 解:(1)∵平行四边形OABC,
解:(1)∵平行四边形OABC,
∴∠BCX=∠AOC,
∵OC=6,B(9,4),
∴tan∠AOC=tan∠BCX=$\frac{4}{3}$;
(2)∵直线DE平分平行四边形OABC的面积,AO=5,
∴AE=CD,即2t-5=0.75t,
解得:t=4,
则当t为4秒时,直线DE平分平行四边形OABC的面积;
(3)∵E(6,4),C(6、0),
∴EC∥y轴,
∴△BEC为RT△BEC,
当△BEP与△BEC相似时;
当P位于如图P2时,∠EBP2=90°,
此时BP2∥EC∥y轴,
∴tan∠AOC=tan∠BEP2=$\frac{4}{3}$,
∵EB=3,
∴BP2=4,
∴P2(9,8);
当P位于如图P1时,∠EP1B=90°,作P1G⊥AB,垂足为G,
∵BP1=3×4÷5=$\frac{12}{5}$,tan∠BEP2=$\frac{4}{3}$,
∴EP1=$\frac{9}{5}$,
∴P1G=$\frac{9}{5}$×$\frac{4}{5}$=$\frac{36}{25}$,EG=$\frac{9}{5}$×$\frac{3}{5}$=$\frac{27}{25}$,
∴P1($\frac{177}{25}$,$\frac{136}{25}$),
综上所述P点坐标为($\frac{177}{25}$,$\frac{136}{25}$)或(9,8).
点评 此题属于相似形综合题,涉及的知识有:坐标与图形性质,相似三角形的判定与性质,锐角三角函数定义,平行四边形的性质,以及平行线的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
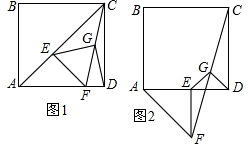
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
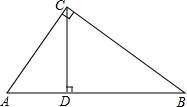 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.则下列等式正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
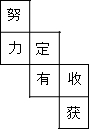 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“定”在正方体的前面,那么这个正方体的后面是( )| A. | 定 | B. | 有 | C. | 收 | D. | 获 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com