
 、1;④1、4、4.可构成直角三角形的有
、1;④1、4、4.可构成直角三角形的有科目:初中数学 来源: 题型:
| A、0种 | B、1种 | C、2种 | D、3种 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).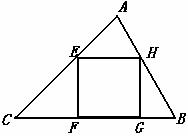
查看答案和解析>>
科目:初中数学 来源:2011年江苏省江阴市九年级上学期期中考试数学卷 题型:解答题
某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:
定义:如果一个正方形的四个顶点都在一个三角形的边上,那么我们就把这个正方形叫做三角形的内接正方形.
结论:在探讨过程中,有三位同学得出如下结果:
甲同学:在钝角、直角、不等边锐角三角形中分别存在____个、____个、_____个大小不同的内接正方形.
乙同学:在直角三角形中,两个顶点都在斜边上的内接正方形的面积较大.
丙同学:在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.
任务:(1)填充甲同学结论中的数据;
(2)乙同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
(3)请你结合(2)的判定,推测丙同学的结论是否正确,并证明。
(如图,设锐角△ABC的三条边分别为 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).

查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏南京) 题型:选择题
一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种 B. 1种 C. 2种 D. 3种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com