解:(1)

,
由①得:y=3x-10 ③,
把③代入②得:x=3,
把x=3代入③得:y=-1,
则原方程组的解为:
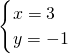
;
(2)

,
①-②得:3p=18,
p=6,
把p=6代入②得:q=-

,
则原方程组的解为:

.
(3)

,
①+②得:7m=14,
m=2,
把m=2代入②得:n=

,
则原方程组的解为:
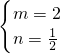
.
(4)

,
①×4-②×3得:11y=55,
y=5,
把y=5代入②得:x=0,
则原方程组的解为:
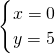
.
(5)

,
①×4-②×3得:y=-

,
把y=-

代入②得:x=

,
则原方程组的解为:
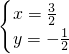
.
(6)

,
由①变形得:3x-2y=8 ③,
②+③得:x=2,
把x=2代入②得:y=-1,
则原方程组的解为:
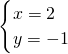
.
(7)

,
由①变形得:3m+2n=78 ③,
由②变形得:4m-3n=36 ④
③×3+④×2得:m=18,
把m=18代入④得:n=12,
则原方程组的解为:

;
(8)

,
由①变形得:3x+5y=6 ③,
由②变形得:5x-3y=2 ④,
③×3+④×5得:x=

,
把x=

代入③得:y=
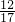
,
则原方程组的解为:

.
(9)

,
由①变形得:8x+15y=54 ③,
由②变形得:4x-5y=2 ④,
③+④×3得:x=3,
把x=3代入④得:y=2,
则原方程组的解为

.
(10)

,
由①变形得:4x-3y=-5 ③,
③-②得:x=-3,
把x=-3代入②得:y=-

,
则原方程组的解为:

.
分析:根据代入消元法和加减消元法的步骤先进行消元,得到关于一个未知数的方程,求出方程的解,再代入其中的一个方程,求出另一个未知数即可.
点评:此题考查了消元法解二元一次方程组,用到的知识点是加减法和代入法,关键是掌握两种方法的步骤.

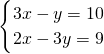
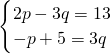
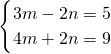
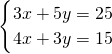
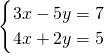
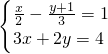
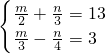
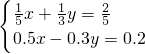
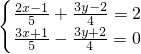
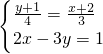 .
. ,
,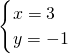 ;
; ,
, ,
, .
. ,
, ,
,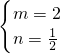 .
. ,
,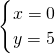 .
. ,
, ,
, 代入②得:x=
代入②得:x= ,
,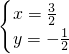 .
. ,
,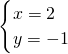 .
. ,
, ;
; ,
, ,
, 代入③得:y=
代入③得:y=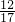 ,
, .
. ,
, .
. ,
, ,
, .
.
