【题目】在同一平面直角坐标系中，函数y=ax+b与y=ax2﹣bx的图象可能是（ ）
A．
B．
C．
D．
【答案】C.
【解析】
试题分析：选项A：一次函数图像经过一、二、三象限，因此a＞0，b＞0，对于二次函数y=ax2﹣bx图像应该开口向上，对称轴在y轴右侧，不合题意，此选项错误；选项B：一次函数图像经过一、二、四象限，因此a＜0，b＞0，对于二次函数y=ax2﹣bx图像应该开口向下，对称轴在y轴左侧，不合题意，此选项错误；
选项C：一次函数图像经过一、二、三象限，因此a＞0，b＞0，对于二次函数y=ax2﹣bx图像应该开口向上，对称轴在y轴右侧，符合题意，此选项正确；选项D：一次函数图像经过一、二、三象限，因此a＞0，b＞0，对于二次函数y=ax2﹣bx图像应该开口向上，对称轴在y轴右侧，不合题意，此选项错误.故选C.
智能训练练测考系列答案
计算高手系列答案科目：初中数学 来源： 题型：
【题目】同学们，在我们进入高中以后，将还会学到下面三角函数公式：
sin (α－β)＝sinαcosβ－cosαsinβ，
cos (α－β)＝cosαcosβ＋sinαsinβ
例：sin 15°＝sin (45°－30°)＝sin 45°cos 30°－cos 45°sin 30°＝
(1)试仿照例题，求出cos 15°的准确值；
(2)我们知道，tanα＝
，试求出tan 15°的准确值．
查看答案和解析>>
科目：初中数学 来源： 题型：
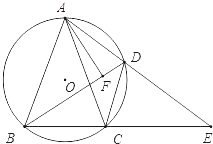
【题目】如图，△ABC内接于⊙O，且AB＝AC，D是
上一点，AD与BC交于E，AF⊥DB，垂足为F．
（1）求证：∠ADB＝∠CDE；
（2）若AF＝DC＝6，AB＝10，求△DBC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
与
轴交于点
和点
，与
轴交于点
，连接
交抛物线的对称轴于点
，
是抛物线的顶点．
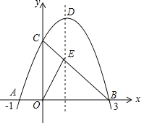
求此抛物线的解析式；
直接写出点和点的坐标；
若点
在第一象限内的抛物线上，且
，求点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
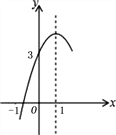
【题目】如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与
轴的一个交点坐标为(－1,0)，其部分图象如图所示，下列结论：
① 4ac<b2；② 方程ax2+bx+c=0的两个根是
；③ 3a+c>0；④ 当y>0时，x的取值范围是-1≤x<3；⑤ 当x<0时，y随x增大而增大；
其中结论正确有__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市销售樱桃，已知樱桃的进价为15元/千克，如果售价为20元/千克，那么每天可售出250千克，如果售价为25元/千克，那么每天可获利2000元，经调查发现：每天的销售量y（千克）与售价x（元/千克）之间存在一次函数关系．
（1）求y与x之间的函数关系式；
（2）若樱桃的售价不得高于28元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
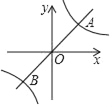
【题目】如图，一次函数y＝x的图象与反比例函数y═
的图象交于A，B两点，且点A坐标为（1，m）．
（1）求此反比例函数的解析式；
（2）当x取何值时，一次函数大于反比例函数的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
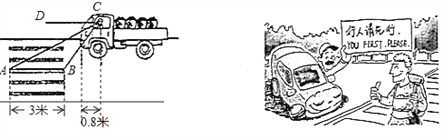
【题目】我国
道路交通安全法
第四十七条规定“机动车行经人行横道时，应当减速行驶；遇行人通过人行横道，应当停车让行” 
如图：一辆汽车在一个十字路口遇到行人时刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是
和
，如果斑马线的宽度是
米，驾驶员与车头的距离是
米，这时汽车车头与斑马线的距离x是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠ACB＝90°，D是边AB的中点，P是边AC上一动点，BP与CD相交于点E．
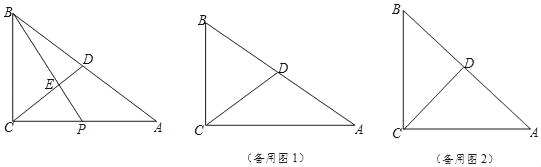
（1）如果BC＝6，AC＝8，且P为AC的中点，求线段BE的长；
（2）联结PD，如果PD⊥AB，且CE＝2，ED＝3，求cosA的值；
（3）联结PD，如果BP2＝2CD2，且CE＝2，ED＝3，求线段PD的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com