
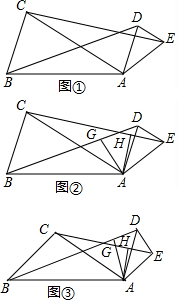
 如图①,在△ABC和△ADE中,AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∠BAC=∠DAE,连接BD、CE.
如图①,在△ABC和△ADE中,AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∠BAC=∠DAE,连接BD、CE.分析 (1)①根据SAS判定△BAD≌△CAE,再根据全等三角形的对应边相等,得出结论即可;②根据全等三角形的性质,得出∠ABG=∠ACH,BG=CH,进而判定△BAG≌△CAH,即可得出结论:AG与AH的数量关系为AG=AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
(2)先判定△BAD∽△CAE,再根据相似三角形的性质,得出$\frac{AB}{AC}$=$\frac{BG}{CH}$=$\frac{3}{2}$,∠ABG=∠ACH,最后判定△BAG∽△CAH,即可得出结论:AG与AH的数量关系为AG=$\frac{3}{2}$AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
解答  解:(1)如图①∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=AC,
解:(1)如图①∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=AC,
∴AD=AE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②AG与AH的数量关系为AG=AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
证明:如图②∵△BAD≌△CAE,
∴∠ABG=∠ACH,
∵DG=$\frac{1}{4}$BD,EH=$\frac{1}{4}$CE,BD=CE,
∴BG=CH,
在△BAG和△CAH中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABG=∠ACH}\\{BG=CH}\end{array}\right.$,
∴△BAG≌△CAH(SAS),
∴AG=AH,∠BAG=∠CAH,
∴∠GAH=∠BAC;
(2)AG与AH的数量关系为AG=$\frac{3}{2}$AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
理由:如图③,根据AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=$\frac{3}{2}$AC,∠BAC=∠DAE,
可得$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{3}{2}$,∠BAD=∠CAE,
∴△BAD∽△CAE,
∴∠ABG=∠ACH,BD=$\frac{3}{2}$CE,
∵DG=$\frac{1}{4}$BD,EH=$\frac{1}{4}$CE,
∴BG=$\frac{3}{2}$CH,
在△BAG和△CAH中,
$\frac{AB}{AC}$=$\frac{BG}{CH}$=$\frac{3}{2}$,∠ABG=∠ACH,
∴△BAG∽△CAH,
∴$\frac{AG}{AH}$=$\frac{AB}{AC}$=$\frac{3}{2}$,∠BAG=∠CAH,
∴AG=$\frac{3}{2}$AH,∠GAH=∠BAC.
点评 本题主要考查了三角形的综合应用,解决问题的关键是掌握全等三角形的判定与性质以及相似三角形的判定与性质,解题时注意:两边及其夹角分别对应相等的两个三角形全等;两组对应边的比相等且夹角对应相等的两个三角形相似.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:填空题
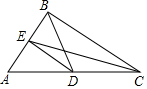 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线,D是AC上的一点且BD=ED,若∠CBD=20°,则∠CED的度数为10°.
如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线,D是AC上的一点且BD=ED,若∠CBD=20°,则∠CED的度数为10°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
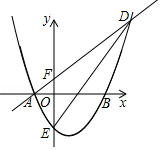 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3).
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com