Question

（本题8分）如图，在数轴上A点表示数a，B点表示数b,AB表示A点和B点之间的距离，且a、b满足．

（1）求A、B两点之间的距离；

（2）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动．设运动的时间为t（秒），

①分别表示甲、乙两小球到原点的距离（用t表示）；

②求甲、乙两小球到原点的距离相等时经历的时间．

 

Answer 1

（1）a=?2,b=6,AB=8（2）①甲到原点的距离：2+t；乙到原点的距离：当0＜t≤3时，6?2t；当t＞3时，2t?6．②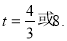

【解析】

试题分析：（1）先根据非负数的性质求出a、b的值，再根据两点间的距离公式即可求得A、B两点之间的距离；（2）①甲球到原点的距离=甲球运动的路程+OA的长，乙球到原点的距离分两种情况：（Ⅰ）当0＜t≤3时，乙球从点B处开始向左运动，一直到原点O，此时OB的长度-乙球运动的路程即为乙球到原点的距离；（Ⅱ）当t＞3时，乙球从原点O处开始向右运动，此时乙球运动的路程-OB的长度即为乙球到原点的距离；

②分两种情况：（Ⅰ）0＜t≤3，（Ⅱ）t＞3，根据甲、乙两小球到原点的距离相等列出关于t的方程，解方程即可．

试题解析：（1）∵|a+2|+（b+3a）2=0，

a+2=0，b+3a=0，

∴a=-2，b=6；

∴AB的距离=|b-a|=8；

（2）①∵甲球运动的路程为：1•t=t，OA=2，

∴甲球与原点的距离为：t+2；

乙球到原点的距离分两种情况：

（Ⅰ）当0＜t≤3时，乙球从点B处开始向左运动，一直到原点O，

∵OB=6，乙球运动的路程为：2•t=2t，

∴乙球到原点的距离为：6-2t；

（Ⅱ）当t＞3时，乙球从原点O处开始一直向右运动，

此时乙球到原点的距离为：2t-6；

②当0＜t≤3时，得t+2=6-2t，

解得t=；

当t＞3时，得t+2=2t-6，

解得t=8．

故当t=秒或t=8秒时，甲乙两小球到原点的距离相等．

考点：1．非负数的性质；2．方程的解法；3．数轴；4．两点间的距离．