
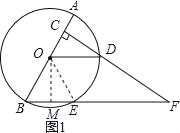
【题目】如图,已知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若点E是![]() 的中点,求∠F的度数;
的中点,求∠F的度数;
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BEEF的值最大?最大值是多少?

【答案】(1)∠F=30°;(2)见解析;(3)当x=![]() 时,最大值=9.
时,最大值=9.
【解析】分析:
(1)如图,连接OE,由OD∥OE可得∠DOE=∠OEB,由点E是![]() 的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
(2)过点O作OM⊥BE于点M,由此可得BE=2BM,再证△OBM≌△DOC可得BM=OC,这样即可得到结论BE=2OC;
(3)由OD∥BF可得△COD∽△CBF,由此可得![]() ,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=
,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=![]() ,从而可得EF=BF-BE=
,从而可得EF=BF-BE=![]() ,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
详解:
(1)如图1,连接OE.
∵![]() ,
,
∴∠BOE=∠EOD,
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)如图1,过O作OM⊥BE于M,
∵OB=OE,
∴BE=2BM,
∵OD∥BF,
∴∠COD=∠B,
在△OBM与△DOC中 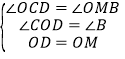 ,
,
∴△OBM≌△DOC,
∴BM=OC,
∴BE=2OC;
(3)∵OD∥BF,
∴△COD∽△CBF,
∴![]() ,
,
∵AC=x,AB=4,
∴OA=OB=OD=2,
∴OC=2﹣x,BE=2OC=4﹣2x,
∴![]() ,
,
∴BF=![]() ,
,
∴EF=BF﹣BE=![]() ,
,
∴BEEF=![]() ,
,
∴当![]() 时,最大值=9.
时,最大值=9.


科目:初中数学 来源: 题型:
【题目】赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中,众数和中位数分别是( )
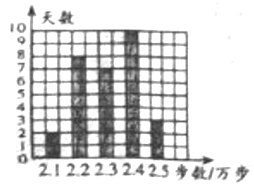
A. 2.2,2.3B. 2.4,2.3C. 2.4,2.35D. 2.3,2.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中E是BC边上一点,且AB=AE,AE,DC的延长线相交于点F.
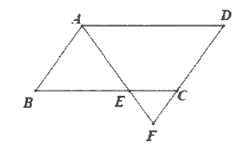
(1)若∠F=62°,求∠D的度数;
(2)若BE=3EC,且△EFC的面积为1,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n)个图案中有白色地砖________块

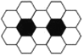
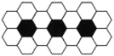
(1) (2) (3)
A.nB.6nC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
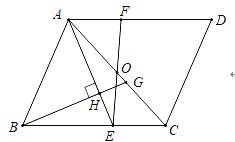
【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点F.过点
于点F.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com