练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在ABCD中，点E、F分别在AB、CD上，且AE=CF．

    （1）求证：△ADE≌△CBF；

    （2）若DF=BF，求证：四边形DEBF为菱形．

    【答案】见解析；菱形

    【解析】试题分析：首先根据平行四边形的性质可得AD=BC，∠A=∠C，再加上条件AE=CF可利用SAS证明△ADE≌△CBF；首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论．

    试题解析：（1）、∵四边形ABCD是平行四边形， ∴AD=BC，∠A=∠C，

    ∵在△ADE和△CBF中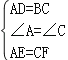，，∴△ADE≌△CBF（SAS）；

    （2）、∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD， ∵AE=CF， ∴DF=EB，

    ∴四边形DEBF是平行四边形， 又∵DF=FB， ∴四边形DEBF为菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】数学课上，老师要求同学们用一副三角板画一个钝角，并且画出它的角平分线．小强的作法如下：
    ①先按照图1的方式摆放一副三角板，画出∠AOB；
    ②在∠AOB处，再按照图2的方式摆放一副三角板，画出射线OC；
    ③去掉三角板后得到的图形如图3．
    老师说小强的作法完全符合要求．

    请你回答：
    （1）小强画的∠AOB的度数是；
    （2）射线OC是∠AOB的平分线的依据是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣a2）3+（﹣a3）2﹣a2a3；
    （2）（3+a）（3﹣a）+a2；
    （3）（x+y﹣3）（x+y+3）；
    （4）（ ）﹣2+（﹣2）3+|﹣3|﹣（π﹣3.14）0 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知梯形的上底为x，下底为9，高为6．

    （1）求梯形面积y与x的关系；
    （2）当y=40时，x为多少？
    （3）当x=0时，y等于多少？此时它表示的是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：a3﹣4a2+3a＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某张日历表上，前三个星期日的日期之和等于42，则该月的1日是星期 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC中，
    （1）AC=BC，∠ACB=90°，CD⊥AB，点E是AB边上一点，点F在线段CE上，且△CBF≌△EBF（如图①），求证：CE平分∠ACD；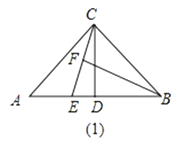
    （2）除去（1）中条件“AC=BC”，其余条件不变（如图②），上述结论是否成立？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列算式的计算结果等于x2－5x－6的是(　　)

    A. (x－6)(x＋1) B. (x＋6)(x－1)

    C. (x－2)(x＋3) D. (x＋2)(x－3)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，△ABC三个顶点的位置如图（每个小正方形的边长均为1）．

    （1）请画出△ABC沿x轴向右平移3个单位长度，再沿y轴向上平移2个单位长度后的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）．
    （2）直接写出A′、B′、C′三点的坐标：
    A′（ ， ）； B′（ ， ）；
    C′（ ， ）．
    （3）求△ABC的面积．

    查看答案和解析>>

    同步练习册答案