
分析 (1)分两种情况:每台的降价不超过500元时,每台的降价超过500元后,由题意直接得出y与x的函数关系式即可;
(2)用每一台冰箱的利润乘以一天销售台数,整理即可得解;
(3)利用配方法根据(2)中的关系式求得答案即可.
解答 解:(1)当x≤500时,y=8+$\frac{x}{50}$×4=$\frac{2}{25}$x+8;
当500<x≤1000时,y=8+$\frac{x}{50}$×10=$\frac{1}{5}$x+8;
(2)由题意得:
当x≤500时,W=($\frac{2}{25}$x+8)(1000-x)=-$\frac{2}{25}$x2+72x+8000;
当500<x≤1000时,W=($\frac{1}{5}$x+8)(1000-x)=-$\frac{1}{5}$x2+192x+8000;
(3)当x≤500时,W=-$\frac{2}{25}$x2+72x+8000=-$\frac{2}{25}$(x-450)2+24200;
当x=450时,W=24200,
当500<x≤1000时,W=-$\frac{1}{5}$x2+192x+8000=-$\frac{1}{5}$(x-480)2+10880;
当x=480时,W=10880,(不合题意),
所以当x=450时,W最大=24200元.
点评 此题主要考查了二次函数的应用以及二次函数的最值问题,根据每天的利润=一件的利润×销售量,建立函数关系式,借助二次函数解决实际问题是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
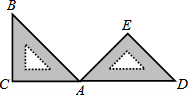 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
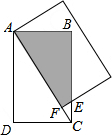 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{21}{4}$ | D. | $\frac{45}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com