
分析 设小艇在静水中的速度是x千米/小时,则顺流速度为x+3千米/小时,逆流速度为x-3千米/小时,根据顺流航行63千米到目的地,然后逆流回航到出发地,航行时间共5小时20分列方程解答;进一步求得顺流航行时间和逆流回航时间即可.
解答 解:设小艇在静水中的速度是x千米/小时,由题意得
$\frac{63}{x+3}$+$\frac{63}{x-3}$=5$\frac{20}{60}$
整理得8x2-189x-72=0,
解得:x1=24,x2=-$\frac{3}{8}$(舍去),
经检验x=24是原分式方程的解,
则顺水航行时间$\frac{63}{x+3}$=$\frac{7}{3}$小时,
逆水航行时间$\frac{63}{x-3}$=3小时,
答:小艇在静水中的速度是24千米/小时,则顺流航行时间为$\frac{7}{3}$小时,逆流航行时为3小时.
点评 此题考查分式方程的实际运用,掌握顺流速度、逆流速度、静水速度、水流速度之间的关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
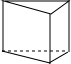 如图所示的是一个棱柱,请问:
如图所示的是一个棱柱,请问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
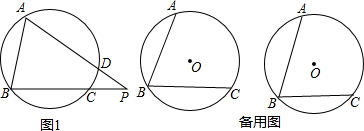
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
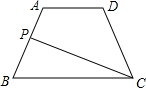 如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.
如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1$\frac{1}{3}$ | B. | -3$\frac{2}{3}$ | C. | -3$\frac{2}{3}$与-1$\frac{2}{3}$ | D. | -3$\frac{2}{3}$与-1$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com