
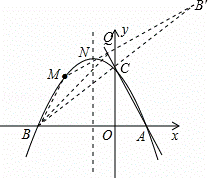
如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,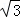 ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,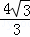 ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
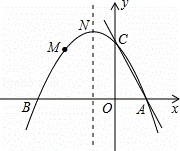
解:(1)由抛物线顶点坐标为N(﹣1,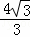 ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+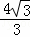 ,
,
将M(﹣2,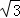 )代入,得
)代入,得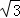 =a(﹣2+1)2+
=a(﹣2+1)2+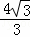 ,
,
解得a=﹣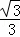 ,
,
故所求抛物线的解析式为y=﹣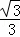 x2﹣
x2﹣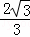 x+
x+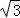 ;
;
(2)∵y=﹣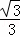 x2﹣
x2﹣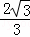 x+
x+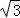 ,
,
∴x=0时,y=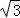 ,
,
∴C(0,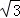 ).
).
y=0时,﹣
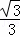 x2﹣
x2﹣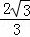 x+
x+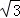 =0,
=0,
解得x=1或x=﹣3,
∴A(1,0),B(﹣3,0),
∴BC=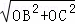 =2
=2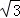 .
.
设P(﹣1,m),显然PB≠PC,所以
当CP=CB时,有CP= =2
=2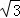 ,解得m=
,解得m=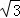 ±
±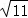 ;
;
当BP=BC时,有BP=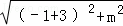 =2
=2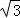 ,解得m=±2
,解得m=±2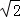 .
.
综上,当△PBC为等腰三角形时,点P的坐标为(﹣1,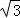 +
+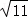 ),(﹣1,
),(﹣1,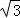 ﹣
﹣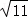 ),(﹣1,2
),(﹣1,2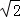 ),(﹣1,﹣2
),(﹣1,﹣2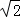 );
);
(3)由(2)知BC=2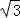 ,AC=2,AB=4,
,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
又BM=2,所以此时△QBM的周长最小.
由B(﹣3,0),C(0,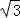 ),易得B′(3,2
),易得B′(3,2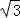 ).
).
设直线MB′的解析式为y=kx+n,
将M(﹣2,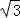 ),B′(3,2
),B′(3,2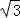 )代入,
)代入,
得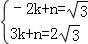 ,解得
,解得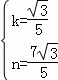 ,
,
即直线MB′的解析式为y=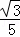 x+
x+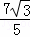 .
.
同理可求得直线AC的解析式为y=﹣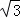 x+
x+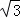 .
.
由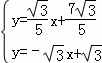 ,解得
,解得 ,即Q(﹣
,即Q(﹣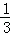 ,
,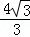 ).
).
所以在直线AC上存在一点Q(﹣ ,
, ),使△QBM的周长最小.
),使△QBM的周长最小.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
下列说法正确的是( )
|
| A. | 多边形的外角和与边数有关 |
|
| B. | 平行四边形既是轴对称图形,又是中心对称图形 |
|
| C. | 当两圆相切时,圆心距等于两圆的半径之和 |
|
| D. | 三角形的任何两边的和大于第三边 |
查看答案和解析>>
科目:初中数学 来源: 题型:
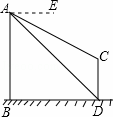
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
四川省“单独两孩”政策于2014年3月20日正式开始实施,该政策的实施可能给我们的生活带来一些变化,绵阳市人口计生部门抽样调查了部分市民(每个参与调查的市民必须且只能在以下6种变化中选择一项),并将调查结果绘制成统计图:
种类 A B C D E F
变化 有利于延缓社会老龄化现象 导致人口暴增 提升家庭抗风险能力 增大社会基本公共服务的压力 环节男女比例不平衡现象 促进人口与社会、资源、环境的协调可持续发展
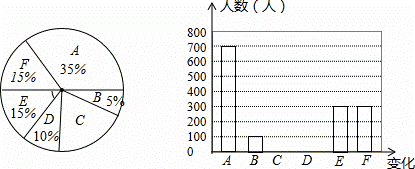
根据统计图,回答下列问题:
(1)参与调查的市民一共有 人;
(2)参与调查的市民中选择C的人数是 人;
(3)∠α= ;
(4)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
某篮球队12名队员的年龄如表:
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和平均数分别是( )
|
| A. | 18,19 | B. | 19,19 | C. | 18,19.5 | D. | 19,19.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com