
 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)分析 (1)先利用切线的性质得出∠GAN=2∠MAN,再求出∠MAN,即可得出结论;
(2)①把三角形ABC绕A旋转120°就能得到图形.
②连接MQ,过M点作MF⊥DE,由AN=3,AC=4,求出NE的长;在Rt△MFQ中,利用勾股定理可求出QF,根据垂径定理知QF就是弧长PQ的一半.
③过M作AD的垂线设垂足为H,然后证MH与⊙M半径的大小关系即可;连接AM、MN,由于AE是⊙M的切线,故MN⊥AE,在Rt△AMN中,通过解直角三角形,易求得∠MAN=30°,由此可证得AM是∠DAE的角平分线,根据角平分线的性质即可得到MH=MN,由此可证得⊙M与AD相切;
(3)分两种情况AC与⊙M相切或旋转过程中,点C在⊙M内部,利用勾股定理即可得出结论.
解答 解:(1)如图1,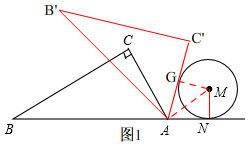
旋转到如图所示的位置时,AC'与⊙M相切于G,
连接MG,
∴∠AGM=90°,
∵AN与⊙M相切于N,
∴∠ANM=90°,
连接AM,
∴∠GAN=2∠MAN,在
Rt△AMN中,MN=$\sqrt{3}$,AN=3,
∴tan∠MAN=$\frac{MN}{AN}$=$\frac{\sqrt{3}}{3}$
∴∠MAN=30°,
∴∠GAN=60°,
∵∠BAC=60°,
∴α=∠CAC'=180°-60°-60°=60°;
∵AN于⊙M相切,所以α=120°
故答案为:60°或120°,
(2)①如图Rt△ADE就是要画的图形,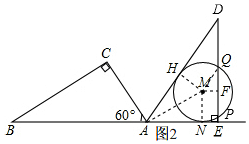
②连接MQ,过M点作MF⊥DE,垂足为F,由Rt△ABC可知,
AC=$\frac{1}{2}$AB,
根据翻折变换的知识得到AC=AE=4,
NE=AE-AN=4-3=1,
在Rt△MFQ中,解得FQ=$\sqrt{2}$,故弦PQ的长度2$\sqrt{2}$.
故答案为:2$\sqrt{2}$
③AD与⊙M相切.
证明:过点M作MH⊥AD于H,连接MN,MA,则MN⊥AE,且MN=$\sqrt{3}$,
在Rt△AMN中,tan∠MAN=$\frac{MN}{AN}=\frac{\sqrt{3}}{3}$,
∴∠MAN=30°,
∵∠DAE=∠BAC=60°,
∴∠MAD=30°,
∴∠MAN=∠MAD=30°,
∴MH=MN,
∴AD与⊙M相切,
(3)在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,
∴AC=4,
在Rt△AMN中,MN=$\sqrt{3}$,AN=3,
∴AM=2$\sqrt{3}$,
∴⊙M上的点到点A的最大距离为2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$>4,
∵边AC与⊙M有一个公共点,
∴AC和⊙M相切或点C在⊙M内,
①AC与⊙M相切时,x是⊙M的半径,
∴x=$\sqrt{3}$,
②当点C刚好落在⊙M上时,
如图3, 连接C'M,AM,过点M作MG⊥AC',
连接C'M,AM,过点M作MG⊥AC',
在Rt△C'MG中,GM2=C'M2-C'G2,
∵AC'=AG+C'G=4,
∴GM2=C'M2-(4-AG)2,
在Rt△AMG中,GM2=AM2-AG2,
∴C'M2-(4-AG)2=AM2-AG2,
∴($\sqrt{3}$)2-(4-AG)2=(2$\sqrt{3}$)2-AG2,
∴AG=$\frac{25}{8}$,
∴x=MG=$\sqrt{12-(\frac{25}{8})^{2}}$=$\frac{\sqrt{143}}{8}$,
∴0≤x<$\frac{\sqrt{143}}{8}$或x=$\sqrt{3}$;
点评 此题是圆的综合题,主要考查了圆的切线,旋转的性质,勾股定理,直角三角形的性质,解本题的关键是画出图形,难点是确定出x的范围,是一道难度比较大的中考常考题.


科目:初中数学 来源: 题型:解答题
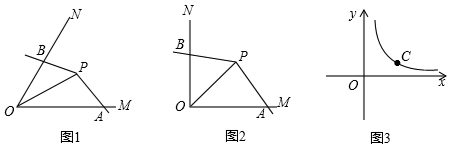 如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
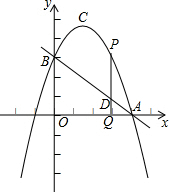 如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
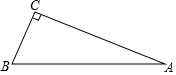 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.
已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC≡∠E=60°,若BE=10,DE=4,则BC的长度是14.
如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC≡∠E=60°,若BE=10,DE=4,则BC的长度是14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com