
【题目】若点A(3,3 )是正比例函数y=x上一点,点M(m,0)与点N(0,n)分别在x轴与y轴上,且∠MAN=90°.
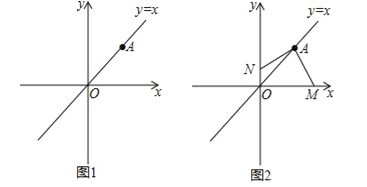
(1)如图1,当N点与原点O重合,求M点的坐标;
(2)如图2,已知m,n都为正数,连接MN,若MN=![]() ,求△MON的面积.
,求△MON的面积.
【答案】(1)M(6,0);(2)![]() .
.
【解析】
试题分析:(1)过点A作AD⊥x轴于D,由点A的坐标即可得出AD=OD=3,进而得出∠AOD=∠OAD=45°,再通过角的计算得出∠AMO=45°,从而得出AO=AM,根据等腰三角形的性质即可得出OM=2OD,由此即可得出点M的坐标;
(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,由点A的坐标结合矩形的性质即可得出四边形APOQ是正方形,根据正方形的性质找出AP=AQ,再根据全等三角形的判定定理(ASA)即可证出△APN≌△AQM,从而得出PN=QM,通过边与边之间的关系结合勾股定理即可得出mn的值,将其代入三角形的面积公式即可得出结论.
试题解析:(1)当N点与原点O重合时,过点A作AD⊥x轴于D,如图3所示.
∵A(3,3),∴AD=OD=3,∴∠AOD=∠OAD=45°.
又∵∠MAN=90°,∴∠AMO=90°﹣45°=45°,∴AO=AM,∴OM=2OD=6,∴M点坐标为(6,0).
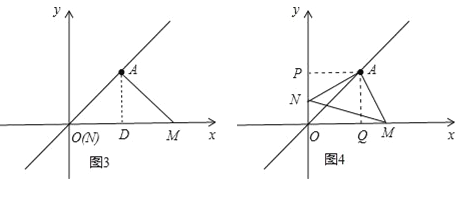
(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,如图4所示.
则∠APO=∠AQO=90°,又∵∠POQ=90°,∴四边形APOQ是矩形,∵A(3,3),∴OP=OQ=3,∴四边形APOQ是正方形,∴AP=AQ.
∵∠PAN+∠NAQ=90°,∠QAM+∠NAQ=90°,∴∠PAN=∠QAM.
在△APN和△AQM中,∵∠APN=∠AQM=90°,AP=AQ,∠PAN=∠QAM,∴△APN≌△AQM(ASA),∴PN=QM.
∵M (m,0),N (0,n),∴ON=n,OM=m,∴PN=3﹣n,QM=m﹣3,∴3﹣n=m﹣3,即m+n=6.
在Rt△MON中,OM2+ON2=MN2,∴![]() ,即m2+n2=30.
,即m2+n2=30.
∵(m+n)2=m2+2mn+n2,∴62=30+2mn,即mn=3,∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场一天中售出李宁牌运动鞋11双,其中各种尺码的鞋的销售量如表所示,则这11双鞋的尺码组成一组数据中位数为_____.
鞋的尺码(单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元;中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.
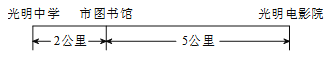
(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式;
(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
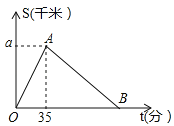
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回中点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=100°,∠ACB=40°,∠ABC的平分线BD交AC于点D,∠ACB的平分线CP交BD于点D.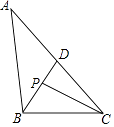
(1)BD与AC的位置关系是 .
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F, 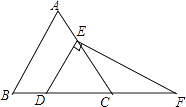
(1)求∠F的度数;
(2)若CD=3,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com