
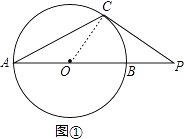
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(1)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(2)如图2,D为 ![]() 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
【答案】
(1)解:如图,连接OC,
∵⊙O与PC相切于点C,
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°﹣∠COP=36°;
(2)解:∵E为AC的中点,
∴OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°﹣∠EAO=80°,
∴∠ACD= ![]() ∠AOD=40°,
∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD﹣∠A=40°﹣10°=30°
【解析】本题考查了切线的性质,解题的关键是能够利用圆的切线垂直于经过切点的半径得到直角三角形,难度不大.(1)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答
案;(2)根据E为AC的中点得到OD⊥AC,从而求得∠AOE=90°﹣∠EAO=80°,然后利用圆周角定理求得∠ACD= ![]() ∠AOD=40°,最后利用三角形的外角的性质求解即可.
∠AOD=40°,最后利用三角形的外角的性质求解即可.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,2)、B(2 ![]() ,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.
,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA. 
(1)当AB∥PQ时,点P的横坐标是;
(2)当BP∥QA时,点P的横坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙M与x轴相切于原点,平行于y轴的直线交圆于P,Q两点,P点在Q点的下方,若P点坐标是(2,1),则圆心M的坐标是( )
A.(0,3)
B.(0,2)
C.(0,![]() )
)
D.(0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在A地往北60m的B处有一幢房,西80m的C处有一变电设施,在BC的中点D处有古建筑.因施工需要在A处进行一次爆破,为使房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,AD与⊙O相切于点B,D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( ) 
A.70°
B.105°
C.100°
D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,使C落在F处,BF交AD于E,则下列结论不一定成立的是( ) 
A.AD=BF
B.△ABE≌FDE
C.sin ![]()
D.△ABE∽△CBD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com