
【题目】如图:在数轴上 A 点表示数 a,B 点示数 b,C 点表示数 c,b 是最大的负整数,且 a、b 满足|a+ 3|+(c﹣6)2=0.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得 A点与B 点重合,则点 C与数 表示的点重合;
(3)点 A、B、C开始在数轴上运动,若点 A以每秒 2个单位长度的速度向左运动,同时,点 B和 点 C分别以每秒1个单位长度和 4个单位长度的速度向右运动,假设 t 秒钟过后,若点 A与点 B之间的距离表示为 AB,点 A与点 C之间的距离表示为 AC,点 B与点 C之间的距离表示为 BC.则 AB= ,AC= ,BC= .(用 含 t的代数式表示)
(4)请问:2BC+AB - ![]() AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
AC的值是否随着时间 t 的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
【答案】(1)-3,-1,6;(2)-10;(3)AB=2+3t,AC=6t+9,BC=7+3t;(4)不变,2.5.
【解析】
(1)利用|a+3|+(c-6)2=0,得a+3=0,c-6=0,解得a,c的值,由b是最大的负整数,可得b=-1;
(2)先求出对称点,然后再求得点C到对称点的距离,从而求得点C的对称点;
(3)利用数轴表示出A、B、C三点表示的数,进而可得AB、AC、BC的长;
(4)根据题意列方程即可得到结论.
(1)∵|a+3|+(c-6)2=0,
∴a+3=0,c-6=0,
∴a=-3,c=6,
∵b是最大的负整数,
∴b=-1;
(2)点A与点B的中点对应的数为:![]() =-2,
=-2,
点C到-2的距离为8,所以与点C重合的数是:-2-8=-10.
(3)AB=t+2t+2=3t+2,
AC=2t+4t+9=6t+9,
BC=(4-1)t+7=3t+7;
(4)∵AB=3t+2,AC=6t+9,BC=3t+7,
∴2BC+AB - ![]() AC=2(3t+7)+3t+2-
AC=2(3t+7)+3t+2-![]() (6t+9)=6t+14+3t+2-9t-13.5=2.5,
(6t+9)=6t+14+3t+2-9t-13.5=2.5,
∴2BC+AB - ![]() AC的值不随着时间t的变化而改变,其值为2.5.
AC的值不随着时间t的变化而改变,其值为2.5.


科目:初中数学 来源: 题型:
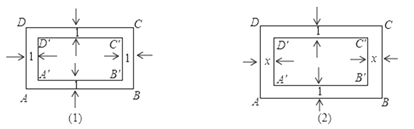
【题目】如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;
(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
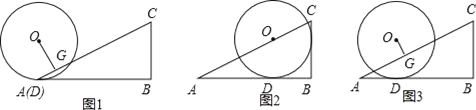
【题目】如图,△ABC中,∠B=90°,tan∠BAC=![]() ,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com