
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.直线MN与l1相交于M;与l2相交于N,⊙O的半径为1,∠1=60°,直线MN从如图位置向右平移,下列结论
①l1和l2的距离为2 ②MN=![]() ③当直线MN与⊙O相切时,∠MON=90°
③当直线MN与⊙O相切时,∠MON=90°
④当AM+BN=![]() 时,直线MN与⊙O相切.正确的个数是( )
时,直线MN与⊙O相切.正确的个数是( )
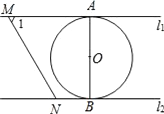
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】分析:本题主要利用切线的性质的判定,切线长定理和直角三角形的性质解决问题.
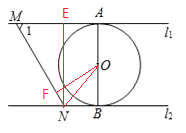
解析:连结OA、OB,根据切线的性质和l1∥l2得到AB为⊙O的直径,则l1和l2的距离为2,故①正确;过点N作NE⊥MA,半径为1,∴AB=2, ∵∠1=60°,∴MN=![]() ,故②正确;当MN与⊙O相切,连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO=∠OMN=30°,∠ONB=∠BNM=60°,∴∠MON=90°,故③正确;∵AE=BN,NE=2, ∵∠1=60°,∴ME=
,故②正确;当MN与⊙O相切,连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO=∠OMN=30°,∠ONB=∠BNM=60°,∴∠MON=90°,故③正确;∵AE=BN,NE=2, ∵∠1=60°,∴ME=![]() ,∵AM+BN=
,∵AM+BN=![]() ,∴BN=
,∴BN=![]() ,过点O作OF⊥MN,连接ON,∵OB=1,∴∠ONB=∠BNM=60°,∴OF=1,∴直线MN与⊙O相切,故④正确.
,过点O作OF⊥MN,连接ON,∵OB=1,∴∠ONB=∠BNM=60°,∴OF=1,∴直线MN与⊙O相切,故④正确.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点. ![]()
(1)若AB=10cm,则MN=cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,M(n)= ![]()
(1)填空:M(5)= , M(50) 是一个数(填“正”或“负”)
(2)计算:①2M(6)+M(7);②4M(7)+2M(8);
(3)直接写出2016M(n)+1008M(n+1)的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果ab<0,那么下列判断正确的是( )
A. a<0,b<0 B. a>0,b>0
C. a≥0,b≤0 D. a<0,b>0或a>0,b<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com