
【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 . 
【答案】y= ![]() x
x
【解析】解:设直线l和10个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C, ∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这10个正方形分成面积相等的两部分,
∴两边分别是5,
∴三角形ABO面积是7,
∴ ![]() OBAB=7,
OBAB=7,
∴AB= ![]() ,
,
∴OC=AB= ![]() ,
,
由此可知直线l经过( ![]() ,3),
,3),
设直线方程为y=kx(k≠0),
则3= ![]() k,解得k=
k,解得k= ![]()
∴直线l解析式为y= ![]() x.
x.
故答案为:y= ![]() x.
x.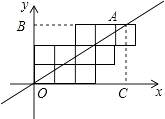
设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,x,y满足:![]() (x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
(x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.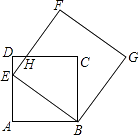
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= ![]() 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在以O为原点的平面直角坐标系中,点A的坐标为(0,2),点P(s,t)在抛物线y= ![]() x2+1上,点P到x轴的距离记为m,PA=n.
x2+1上,点P到x轴的距离记为m,PA=n.
(1)若s=4,分别求出m、n的值,并比较m与n的大小关系;
(2)若点P是该抛物线上的一个动点,则(1)中m与n的大小关系是否仍成立?请说明理由;
(3)如图2,过点P的直线y=kx(k≠0)与抛物线交于另一点Q连接PA、QA,是否存在k使得PA=2QA?若存在,请求出k的值;若不存在,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
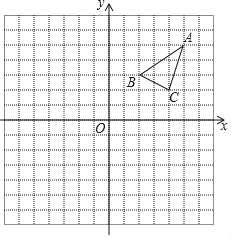
【题目】已知△ABC在平面直角坐标系中的位置如图所示,
(1)先画出△ABC关于x轴对称的图形△A1B1C1,再画出△A1B1C1关于y轴对称的图形△A2B2C2;
(2)直接写出△A2B2C2各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
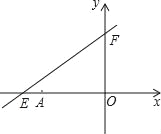
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,Rt△ABC中,∠ABC=90°,AD平分∠BAC交BC于D. 
(1)用尺规画圆O,使圆O过A、D两点,且圆心O在边AC上.(保留作图痕迹,不写作法)
(2)求证:BC与圆O相切;
(3)设圆O交AB于点E,若AE=2,CD=2BD.求线段BE的长和弧DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com