练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．在一个不透明的袋子中，装有3个完全相同的小球，把它们分别标号为1，2，3．在看不到球的条件下，随机摸出一个小球后放回，再随机摸出一个小球．则两次摸出的小球的标号相同的概率是$\frac{1}{3}$．

    分析 画出树状图，然后根据概率公式计算即可得解．

    解答 解：根据题意画出树状图如下：

    共有9种情况，两次摸出的小球的标号相同的有3种，
    所以P（两次摸出的小球的标号相同）=$\frac{3}{9}=\frac{1}{3}$，
    故答案为：$\frac{1}{3}$．

    点评 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．若$\sqrt{{a^2}-3a+1}$+b2-2b+1=0，则${a^2}+\frac{1}{a^2}$-|b|的值为（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．因式分解：（a+b）（a2-ab+b2）-（a+b）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（-2）7×（$\frac{1}{2}$-$\frac{3}{4}$-$\frac{1}{8}$）；
    （2）（-3）4÷$\frac{9}{4}$×$\frac{4}{9}$+（-16）
    （3）-2÷2+（-2）÷（-$\frac{1}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

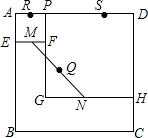    17．如图，四边形ABCD是边长为8的正方形，点R、S在边AD上，且AR=1，SD=2，点P是线段RS上的动点，分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD，M、N分别为EF、GH的中点．连结MN，设MN的中点为0，则当点P从点R运动到点S时，点O移动的路径长为2.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列命题中，是真命题的是（　　）
    A．任何一个三角形都有且只有一个外接圆
    B．任何一组数据的中位数和平均数都不会相等
    C．对角线相等且互相垂直的四边形是矩形
    D．位似变换不改变图形的形状和大小

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，直线y=kx+b经过点A（2，1），则下列结论中正确的是（　　）
    A．当y≤2时，x≤1B．当y≤1时，x≤2C．当y≥2时，x≤1D．当y≥1时，x≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．为鼓励人们节约用水，某地实行阶梯式计量水价（如下表所示）．
    级别月用水量水价
    第1级20吨以下（含20吨）1.6元/吨
    第2级20吨-30吨（含30吨）超过20吨部分按2.4元/吨
    第3级30吨以上超过30吨部分按4.8元/吨
    （1）若张红家5月份用水量为15吨，则该月需缴交水费24元；
    （2）若张红家6月份缴交水费44元，则该月用水量为25吨；
    （3）若张红家7月份用水量为a吨（a＞30），请计算该月需缴交水费多少元？（用含a的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）计算：（$\frac{1}{2}$）-2+$\sqrt{4}$-2cos60°；
    （2）先化简，再求值：（a-$\frac{1}{a}$）÷$\frac{a+1}{a}$，其中a=$\sqrt{3}$+1．

    查看答案和解析>>

    同步练习册答案