解:过点A作BC边上的高AM,垂足为M,交DE于N.
∵AB=10,sinB=

,
∴AM=ABsinB=6,
∵DE∥BC,
∴△ADE∽△ABC,
∴
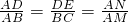
,即
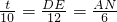
,
∴DE=

t,AN=

t,MN=6-

t.
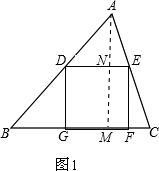
(1)当正方形DEFG的边GF在BC上时,如图1,
DE=DG=MN,即

t=6-

t,
∴t=

,
∴当t=

时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,如图2,
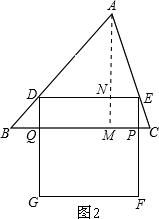
S
△CEP+S
△BDQ=
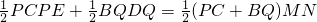
=
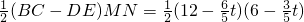
S
△ABC=
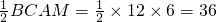
令

(12-

t)(6-

t)=

×36,
解得t
1=15(舍去),t
2=5,
∴当t=5时,△CEP与△BDQ的面积之和等于△ABC面积的

;
(3)分两种情况:
①当正方形DEFG在△ABC的内部时,如图3,
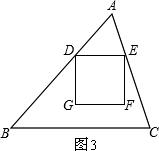
S=DE
2=(

t)
2=
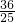
t
2,此时t的范围是0≤t≤

,
当t=

时,S的最大值为16.
②当正方形DEFG的一部分在△ABC的外部时,
如图2,S=DE•MN=

t(6-

t)=-
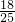
t
2+

t,此时t的范围是

<t≤10,
∵-
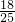
<0,∴当t=5时,S的最大值为18,
∵18>16,∴S的最大值为18.
分析:(1)根据题意作辅助线,然后根据相似三角形比例关系即可得出t的值;
(2)根据题意将三角形面积用t表示出来,然后解方程即可;
(3)分两种情况讨论得出答案.
点评:本题主要考查了作辅助线、相似三角形的证明及性质、二次函数最值及正方形的性质,难度较大.

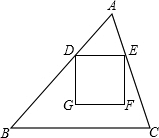 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t, ?
? ,
,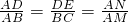 ,即
,即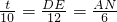 ,
, t,AN=
t,AN= t,MN=6-
t,MN=6- t.
t.
 t=6-
t=6- t,
t, ,
, 时,正方形DEFG的边GF在BC上;
时,正方形DEFG的边GF在BC上;
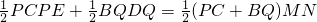
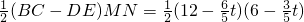
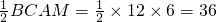
 (12-
(12- t)(6-
t)(6- t)=
t)= ×36,
×36, ;
;
 t)2=
t)2=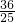 t2,此时t的范围是0≤t≤
t2,此时t的范围是0≤t≤ ,
, 时,S的最大值为16.
时,S的最大值为16. t(6-
t(6- t)=-
t)=-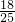 t2+
t2+ t,此时t的范围是
t,此时t的范围是 <t≤10,
<t≤10,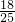 <0,∴当t=5时,S的最大值为18,
<0,∴当t=5时,S的最大值为18,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为