
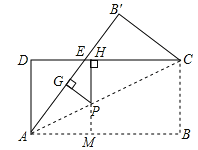
【题目】如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.

(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
【答案】(1)△AED≌△CEB′;证明见解析;(2)4.
【解析】
试题分析:(1)由折叠的性质知,CB′=BC=AD,∠B=∠B′=∠D=90°,∠B′EC=DEA,则由AAS得到△AED≌△CEB′;
(2)延长HP交AB于M,则PM⊥AB,PG=PM,PG+PH=HM=AD,∵CE=AE=CD-DE=8-3=5在Rt△ADE中,由勾股定理得到AD=4,∴PG+PH=HM=AD=4.
试题解析:(1)△AED≌△CEB′
证明:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
又∵∠B′EC=∠DEA,
∴△AED≌△CEB′;
(2)由折叠的性质可知,∠EAC=∠CAB,
∵CD∥AB,
∴∠CAB=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC=8-3=5.
在△ADE中,AD=![]() =4,
=4,
延长HP交AB于M,则PM⊥AB,
∴PG=PM.
∴PG+PH=PM+PH=HM=AD=4.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
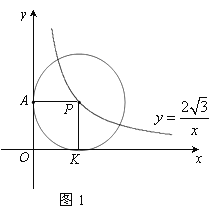
【题目】在直角坐标系xoy中,已知点P是反比例函数![]() 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
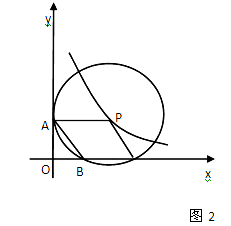
①求出点A,B,C的坐标.
②在P点右侧的反比例函数![]() 图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由.
图像是否存在上点M,使△MBP的面积等于菱形ABCP面积.若存在,试求出满足条件的M点的坐标,若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三只乒乓球上,分别写有三个不同的正整数(用a、b、c表示),三只乒乓球除标的数字不同外,其余都相同,将三只乒乓球放在一个不透明的盒中搅拌均匀,无放回的从中依次摸出2只乒乓球,将球上面的数字相加求和.当和为偶数时,记为事件A,当和为奇数时,记为事件B.
(1)设计一组a、b、c的值,使得事件A为必然发生的事件.
(2)设计一组a、b、c的值,使得事件B发生的概率大于事件A发生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把-6-(+7)+(-2)-(-9)写成省略加号和的形式后的式子是( )
A. -6-7+2-9 B. -6-7-2+9 C. -6+7-2-9 D. -6+7-2+9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com