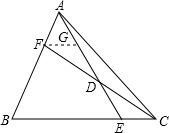
解:(1)如图,过点F作FG∥BC交AE于G,
则∠DFG=∠DCE,∠DGF=∠DEC,
∵D是CF的中点,
∴CD=DF,
在△DCE和△DFG中,
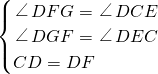
,
∴△DCE≌△DFG(AAS),
∴EC=GF,
∵BF:AF=m:n,
∴
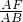
=

,
∵FG∥BC,
∴△AFG∽△ABE,
∴
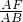
=
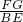
=

,
∴BE:EC=
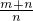
;
(2)若BE=2EC,则BE:EC=2,
由(1)知,
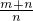
=2,
解得m=n,
∴点F是AB的中点,
∵AC=BC,
∴CF⊥AB;
(3)不能.
理由如下:假设点E能成为BC中点,
则BE=EC,
∴BE:EC=1,
由(1)知
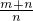
=1,
解得m=0,
这与m、n>0相矛盾,
所以,点E不能成为BC中点.
分析:(1)过点F作FG∥BC交AE于G,根据两直线平行,内错角相等可得∠DFG=∠DCE,∠DGF=∠DEC,再根据中点定义可得CD=DF,然后利用“角角边”证明△DCE和△DFG全等,根据全等三角形对应边相等可得EC=GF,然后求出
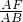
,再求出△AFG和△ABE相似,根据相似三角形对应边成比例列式求解即可得到
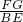
,从而得到BE:EC;
(2)求出BE:EC,然后代入(1)的关系式计算即可求出m=n,从而得到点F是AB的中点,再根据等腰三角形三线合一的性质解答;
(3)假设成立,求出BE:EC,然后代入(1)的关系式计算即可求出m=0,与已知条件矛盾.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线,构造出全等三角形和相似三角形是解题的关键.

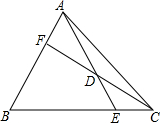 如图,在△ABC中,AC=BC,F为边AB上的一点,BF:AF=m:n(m、n>0),取CF的中点D,连结AD并延长交BC于点E.
如图,在△ABC中,AC=BC,F为边AB上的一点,BF:AF=m:n(m、n>0),取CF的中点D,连结AD并延长交BC于点E. 解:(1)如图,过点F作FG∥BC交AE于G,
解:(1)如图,过点F作FG∥BC交AE于G,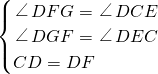 ,
,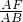 =
= ,
,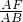 =
=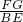 =
= ,
,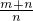 ;
;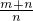 =2,
=2,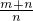 =1,
=1,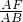 ,再求出△AFG和△ABE相似,根据相似三角形对应边成比例列式求解即可得到
,再求出△AFG和△ABE相似,根据相似三角形对应边成比例列式求解即可得到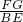 ,从而得到BE:EC;
,从而得到BE:EC;

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为