
| a |
| a2-2a+1 |
| a+1 |
| a2-1 |
|
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
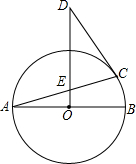 如图,已知AB是⊙O的直径,DO⊥AB于点O,CD是⊙O的切线,切点为C,连接AC,交OD于点E.
如图,已知AB是⊙O的直径,DO⊥AB于点O,CD是⊙O的切线,切点为C,连接AC,交OD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
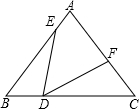 如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F
如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F查看答案和解析>>
科目:初中数学 来源: 题型:
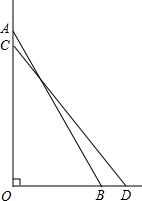 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.查看答案和解析>>
科目:初中数学 来源: 题型:
| 种植种类 | 成本(万元/亩) | 销售额(万元/亩) |
| 甲 | 2.4 | 3 |
| 乙 | 2 | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com