
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.

(1)证明见解析;(2) .
.
【解析】
试题分析:(1)先证得△ADB≌△CDB求得∠ADDF=∠BAD,所以AB∥FD,因为BD⊥AC,AF⊥AC,所以AF∥BD,即可证得.
(2)先证得平行四边形是菱形,然后根据勾股定理即可求得.
试题解析:解:(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC.
∵在△ADB与△CDB中,AB=BC,AD=DC,DB=DB,
∴△ADB≌△CDB(SSS).∴∠BCD=∠BAD.
∵∠BCD=∠ADF,∴∠BAD=∠ADF.∴AB∥FD.
∵BD⊥AC,AF⊥AC,∴AF∥BD.
∴四边形ABDF是平行四边形.
(2)∵四边形ABDF是平行四边形,AF=DF=5,
∴?ABDF是菱形.∴AB=BD=5.
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,
∵AD=6,∴52﹣x2=62﹣(5﹣x)2,解得:x= ,即BE=
,即BE= .
.
∴
 =
= ,
,
∴AC=2AE= .
.
考点:1.平行四边形、菱形的判定和性质;2.线段垂直平分线的性质;3.勾股定理.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:2014-2015山东省威海市环翠区八年级上学期期中考试数学试卷(解析版) 题型:选择题
关于 的分式方程
的分式方程 ,下列说法正确的是 ( )
,下列说法正确的是 ( )
(A)方程的解是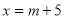
(B)m<-5时,方程的解是正数
(C)m<-5时,方程的解是负数
(D)无法确定
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:选择题
支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北.据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学记数法表示为( )
A.4.73×108 B.4.73×109 C.4.73×1010 D.4.73×1011
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东卷)数学(解析版) 题型:解答题
某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价:(利润率= )
)
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:填空题
如图,双曲线 经过Rt△BOC斜边上的点A,且满足
经过Rt△BOC斜边上的点A,且满足 ,与BC交于点D,S△BOD=21,求k= .
,与BC交于点D,S△BOD=21,求k= .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:选择题
如图,△ABC和△DEF中,AB=DE、角∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )

A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据: .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com