
【题目】动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)
探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系.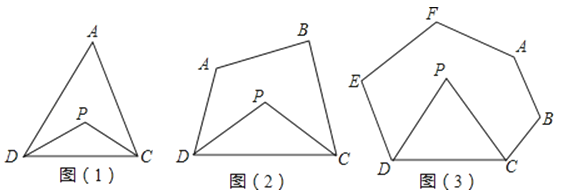
【答案】解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠EDC﹣
∠EDC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠EDC+∠ACD),
(∠EDC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.
【解析】探究一:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理探究解答即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
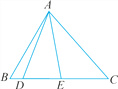
【题目】如图,图中共有_______个三角形,以AD为边的三角形有_________________,以E为顶点的三角形有___________,∠ADB是______的内角,△ADE的三个内角分别是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用普查方式的是( )
A. 调查某班级的每一个同学所穿鞋子的尺码情况
B. 调查某批次烟花爆竹的燃放效果
C. 调查奶茶市场上奶茶的质量情况
D. 调查重庆中学生心里健康现状
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
A. a=1.5,b=2,c=3 B. a=7,b=24,c=25
C. a=6,b=8,c=10 D. a=0.3,b=0.4,c=0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是______(从“条形图,扇形图,折线图和直方图”中选一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论不正确的是( )
A.若a<0,b>0,则a-b<0
B.若a>0,b<0,则a-b>0
C.若a<0,b<0,则a-(-b)>0
D.若a<0,b<0,且|a|>|b|,则a-b<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com